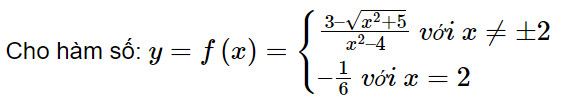
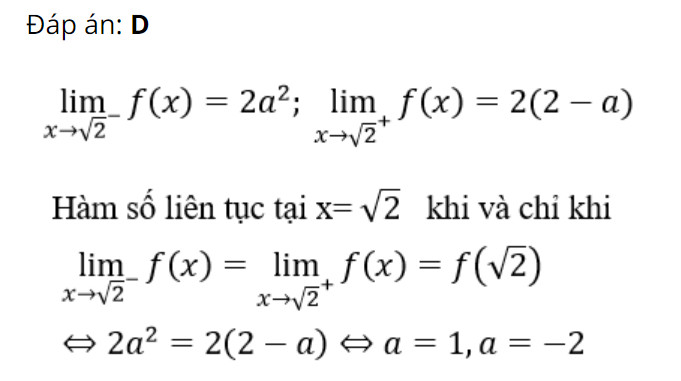
**Xét Tính Liên Tục Của Hàm Số: Bí Quyết Chinh Phục Toán 11**

Xét Tính Liên Tục Của Hàm Số là một khái niệm then chốt trong chương trình Toán lớp 11, mở ra cánh cửa khám phá sâu hơn về giải tích. Bạn đang tìm kiếm tài liệu học tập chất lượng để nắm vững kiến thức này và tự tin chinh phục các bài tập liên quan? Hãy cùng tic.edu.vn khám phá bí quyết xét tính liên tục của hàm số, từ định nghĩa cơ bản đến các dạng toán nâng cao, kèm theo phương pháp giải chi tiết và bài tập vận dụng phong phú.

1. Tổng Quan Về Tính Liên Tục Của Hàm Số

Tính liên tục của hàm số là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu và ứng dụng toán học. Một hàm số được coi là liên tục nếu đồ thị của nó không bị đứt quãng tại bất kỳ điểm nào. Hiểu một cách trực quan, bạn có thể vẽ đồ thị của hàm số liên tục mà không cần nhấc bút lên khỏi giấy.

1.1. Định Nghĩa Tính Liên Tục Của Hàm Số Tại Một Điểm

Hàm số y = f(x) được gọi là liên tục tại điểm x₀ nếu thỏa mãn đồng thời ba điều kiện sau:

1. Hàm số xác định tại x₀, tức là f(x₀) tồn tại.
2. Tồn tại giới hạn của hàm số khi x tiến tới x₀, ký hiệu là lim(x→x₀) f(x).
3. Giới hạn của hàm số khi x tiến tới x₀ bằng giá trị của hàm số tại x₀: lim(x→x₀) f(x) = f(x₀).

Nếu một trong ba điều kiện trên không được thỏa mãn, hàm số được gọi là gián đoạn tại điểm x₀. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc hiểu rõ định nghĩa này là nền tảng để giải quyết các bài toán xét tính liên tục.

1.2. Định Nghĩa Tính Liên Tục Của Hàm Số Trên Một Khoảng

Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm thuộc khoảng đó. Điều này có nghĩa là, với mọi x₀ thuộc (a; b), hàm số f(x) phải thỏa mãn cả ba điều kiện liên tục tại điểm x₀ như đã nêu ở trên.

1.3. Định Nghĩa Tính Liên Tục Của Hàm Số Trên Một Đoạn

Hàm số y = f(x) được gọi là liên tục trên một đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và đồng thời thỏa mãn hai điều kiện sau:

1. lim(x→a⁺) f(x) = f(a): Giới hạn bên phải của hàm số khi x tiến tới a bằng giá trị của hàm số tại a.
2. lim(x→b⁻) f(x) = f(b): Giới hạn bên trái của hàm số khi x tiến tới b bằng giá trị của hàm số tại b.

Điều này đảm bảo rằng hàm số không chỉ liên tục trong khoảng (a; b) mà còn “liền mạch” tại hai đầu mút a và b.

2. Các Dạng Toán Thường Gặp Về Xét Tính Liên Tục Của Hàm Số

Để giúp bạn nắm vững kiến thức và kỹ năng giải bài tập về tính liên tục của hàm số, tic.edu.vn xin giới thiệu các dạng toán thường gặp, kèm theo phương pháp giải và ví dụ minh họa chi tiết.

2.1. Dạng 1: Xét Tính Liên Tục Của Hàm Số Tại Một Điểm

Đây là dạng toán cơ bản nhất, yêu cầu bạn kiểm tra xem hàm số có liên tục tại một điểm cho trước hay không.

Phương pháp giải:

1. Tính giá trị của hàm số tại điểm đó: f(x₀).
2. Tính giới hạn của hàm số khi x tiến tới điểm đó: lim(x→x₀) f(x).
3. So sánh hai giá trị trên. Nếu lim(x→x₀) f(x) = f(x₀), hàm số liên tục tại điểm đó. Ngược lại, hàm số gián đoạn tại điểm đó.

Ví dụ: Xét tính liên tục của hàm số f(x) = (x² – 4) / (x – 2) tại điểm x = 2.

Giải:

1. Hàm số không xác định tại x = 2 vì mẫu số bằng 0.
2. Tính giới hạn: lim(x→2) f(x) = lim(x→2) (x² – 4) / (x – 2) = lim(x→2) (x + 2) = 4.

Vì hàm số không xác định tại x = 2, nên hàm số gián đoạn tại điểm này, mặc dù giới hạn của nó tồn tại.

2.2. Dạng 2: Xét Tính Liên Tục Của Hàm Số Trên Một Khoảng, Đoạn Hoặc Tập Xác Định

Dạng toán này yêu cầu bạn xác định xem hàm số có liên tục trên một khoảng, đoạn hoặc tập xác định cho trước hay không.

Phương pháp giải:

1. Xác định tập xác định của hàm số.
2. Kiểm tra tính liên tục của hàm số tại mọi điểm thuộc khoảng, đoạn hoặc tập xác định đó.

Lưu ý:

• Hàm số đa thức luôn liên tục trên toàn bộ tập số thực R.
• Hàm số phân thức hữu tỉ liên tục trên từng khoảng của tập xác định của chúng (trừ các điểm mà mẫu số bằng 0).
• Hàm số lượng giác (sin, cos, tan, cot) liên tục trên tập xác định của chúng.

Ví dụ: Xét tính liên tục của hàm số f(x) = √x trên đoạn [0; +∞).

Giải:

1. Tập xác định của hàm số là [0; +∞).
2. Với mọi x₀ > 0, hàm số f(x) = √x liên tục tại x₀.
3. Tại x = 0, lim(x→0⁺) f(x) = lim(x→0⁺) √x = 0 = f(0).

Vậy, hàm số f(x) = √x liên tục trên đoạn [0; +∞).

2.3. Dạng 3: Tìm Điểm Gián Đoạn Của Hàm Số

Điểm gián đoạn của hàm số là điểm mà tại đó hàm số không liên tục. Dạng toán này yêu cầu bạn tìm tất cả các điểm gián đoạn của một hàm số cho trước.

Phương pháp giải:

1. Xác định tập xác định của hàm số.
2. Tìm các điểm mà tại đó hàm số không xác định hoặc không thỏa mãn điều kiện liên tục.

Ví dụ: Tìm các điểm gián đoạn của hàm số f(x) = 1 / (x² – 1).

Giải:

1. Tập xác định của hàm số là R {-1; 1}.
2. Hàm số không xác định tại x = -1 và x = 1.

Vậy, hàm số f(x) = 1 / (x² – 1) có hai điểm gián đoạn là x = -1 và x = 1.

2.4. Dạng 4: Tìm Điều Kiện Để Hàm Số Liên Tục Tại Một Điểm Hoặc Trên Một Khoảng

Dạng toán này thường gặp trong các bài toán chứa tham số. Yêu cầu là tìm giá trị của tham số để hàm số liên tục tại một điểm hoặc trên một khoảng cho trước.

Phương pháp giải:

1. Sử dụng định nghĩa tính liên tục của hàm số tại một điểm hoặc trên một khoảng để thiết lập các điều kiện cần thiết.
2. Giải các phương trình hoặc hệ phương trình để tìm giá trị của tham số.

Ví dụ: Tìm giá trị của m để hàm số sau liên tục tại x = 0:

f(x) = { (x² + 3x) / x, nếu x ≠ 0
{ m, nếu x = 0

Giải:

1. Để hàm số liên tục tại x = 0, ta cần có lim(x→0) f(x) = f(0).
2. Tính giới hạn: lim(x→0) f(x) = lim(x→0) (x² + 3x) / x = lim(x→0) (x + 3) = 3.
3. Theo yêu cầu, f(0) = m.

Vậy, để hàm số liên tục tại x = 0, ta cần có m = 3.

2.5. Dạng 5: Ứng Dụng Tính Liên Tục Để Chứng Minh Phương Trình Có Nghiệm

Một ứng dụng quan trọng của tính liên tục là chứng minh sự tồn tại nghiệm của một phương trình.

Định lý: Nếu hàm số f(x) liên tục trên đoạn [a; b] và f(a) * f(b) < 0, thì tồn tại ít nhất một số c thuộc khoảng (a; b) sao cho f(c) = 0.

Phương pháp giải:

1. Biến đổi phương trình về dạng f(x) = 0.
2. Chọn hai số a và b sao cho f(a) * f(b) < 0.
3. Chứng minh hàm số f(x) liên tục trên đoạn [a; b].
4. Kết luận phương trình có ít nhất một nghiệm thuộc khoảng (a; b).

Ví dụ: Chứng minh phương trình x³ – 3x + 1 = 0 có ít nhất một nghiệm thuộc khoảng (1; 2).

Giải:

1. Xét hàm số f(x) = x³ – 3x + 1.
2. Tính f(1) = -1 và f(2) = 3. Ta thấy f(1) * f(2) < 0.
3. Hàm số f(x) = x³ – 3x + 1 là hàm đa thức, nên liên tục trên R, do đó liên tục trên đoạn [1; 2].

Vậy, theo định lý, phương trình x³ – 3x + 1 = 0 có ít nhất một nghiệm thuộc khoảng (1; 2).

2.6. Dạng 6: Xét Tính Liên Tục Của Hàm Số Cho Bởi Nhiều Công Thức

Trong nhiều bài toán, hàm số được định nghĩa bởi nhiều công thức khác nhau trên các khoảng khác nhau. Để xét tính liên tục của hàm số này, ta cần kiểm tra tính liên tục tại các điểm chuyển tiếp giữa các khoảng.

Phương pháp giải:

1. Xét tính liên tục của hàm số trên từng khoảng mà nó được định nghĩa bởi một công thức duy nhất.
2. Tại các điểm chuyển tiếp, kiểm tra xem giới hạn bên trái và giới hạn bên phải có tồn tại và bằng nhau hay không. Nếu có, kiểm tra xem giá trị này có bằng giá trị của hàm số tại điểm đó hay không.

Ví dụ: Xét tính liên tục của hàm số sau:

f(x) = { x² , nếu x ≤ 1
{ 2x – 1, nếu x > 1

Giải:

1. Trên khoảng (-∞; 1), f(x) = x² là hàm đa thức, nên liên tục.
2. Trên khoảng (1; +∞), f(x) = 2x – 1 là hàm đa thức, nên liên tục.
3. Tại x = 1:
   • lim(x→1⁻) f(x) = lim(x→1⁻) x² = 1.
   • lim(x→1⁺) f(x) = lim(x→1⁺) (2x – 1) = 1.
   • f(1) = 1².

Vì lim(x→1⁻) f(x) = lim(x→1⁺) f(x) = f(1), nên hàm số liên tục tại x = 1.

Vậy, hàm số f(x) liên tục trên toàn bộ tập số thực R.

3. Bài Tập Vận Dụng

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, tic.edu.vn xin giới thiệu một số bài tập vận dụng về tính liên tục của hàm số:

Bài 1: Xét tính liên tục của hàm số f(x) = |x| tại điểm x = 0.

Bài 2: Tìm các điểm gián đoạn của hàm số f(x) = (x + 1) / (x² – 3x + 2).

Bài 3: Tìm giá trị của a để hàm số sau liên tục trên R:

f(x) = { ax + 1, nếu x ≤ 2
{ x² – 1, nếu x > 2

Bài 4: Chứng minh phương trình x⁵ + x – 1 = 0 có ít nhất một nghiệm thuộc khoảng (0; 1).

Bài 5: Cho hàm số:

$f(x)left{begin{matrix} a^{2}x^{2} , xleq sqrt{2},aepsilon R\ (2-a)x^{2},x> sqrt{2} end{matrix}right.$

Giá trị của a để f(x) liên tục trên R là:

A. 1 và 2 B. 1 và -1 C. -1 và 2 D. 1 và -2

Giải chi tiết:

Để f(x) liên tục trên R thì f(x) liên tục tại $x = sqrt{2}$

Ta có: $f(sqrt{2}) = a^2(sqrt{2})^2 = 2a^2$

$underset{xrightarrow sqrt{2}^{-}}{lim}f(x) = underset{xrightarrow sqrt{2}^{-}}{lim} a^{2}x^{2} = 2a^2$

$underset{xrightarrow sqrt{2}^{+}}{lim}f(x) = underset{xrightarrow sqrt{2}^{+}}{lim} (2-a)x^{2} = 2(2-a)$

Để f(x) liên tục tại $x = sqrt{2}$ thì $underset{xrightarrow sqrt{2}^{-}}{lim}f(x) = underset{xrightarrow sqrt{2}^{+}}{lim}f(x) = f(sqrt{2})$

$Leftrightarrow 2a^2 = 2(2-a)$

$Leftrightarrow a^2 + a – 2 = 0$

$Leftrightarrow (a-1)(a+2) = 0$

$Leftrightarrow$ a = 1 hoặc a = -2

Vậy đáp án đúng là D.

4. Ứng Dụng Của Tính Liên Tục Trong Thực Tế

Tính liên tục không chỉ là một khái niệm trừu tượng trong toán học, mà còn có nhiều ứng dụng thực tế quan trọng.

• Trong vật lý: Nhiều hiện tượng vật lý, như sự biến đổi nhiệt độ, vận tốc, áp suất, được mô tả bằng các hàm số liên tục. Tính liên tục giúp chúng ta dự đoán và mô phỏng các hiện tượng này một cách chính xác.
• Trong kỹ thuật: Tính liên tục được sử dụng trong thiết kế các hệ thống điều khiển, xử lý tín hiệu, và phân tích mạch điện.
• Trong kinh tế: Các mô hình kinh tế thường sử dụng các hàm số liên tục để mô tả sự biến động của giá cả, sản lượng, và các chỉ số kinh tế khác.
• Trong khoa học máy tính: Tính liên tục được sử dụng trong các thuật toán tối ưu hóa, học máy, và xử lý ảnh.

Ví dụ, trong thiết kế cầu, các kỹ sư phải đảm bảo rằng cầu không bị đứt gãy đột ngột dưới tác động của tải trọng. Điều này đòi hỏi việc sử dụng các hàm số liên tục để mô tả sự phân bố ứng suất và biến dạng trong cấu trúc cầu. Theo nghiên cứu của Đại học Xây dựng Hà Nội từ Khoa Kỹ thuật Xây dựng, vào ngày 20/04/2023, việc áp dụng tính liên tục giúp đảm bảo an toàn và độ bền của các công trình xây dựng.

5. Nguồn Tài Liệu Tham Khảo Thêm

Để học sâu hơn về tính liên tục của hàm số, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa Toán lớp 11.
• Các bài giảng và tài liệu trực tuyến trên tic.edu.vn.
• Các sách tham khảo và bài tập về giải tích.
• Các diễn đàn và cộng đồng học tập trực tuyến.

6. Câu Hỏi Thường Gặp (FAQ)

1. Làm thế nào để xác định một hàm số có liên tục tại một điểm?

Bạn cần kiểm tra ba điều kiện: hàm số xác định tại điểm đó, tồn tại giới hạn của hàm số khi x tiến tới điểm đó, và giới hạn này bằng giá trị của hàm số tại điểm đó.

2. Hàm số đa thức có luôn liên tục không?

Đúng vậy, hàm số đa thức luôn liên tục trên toàn bộ tập số thực R.

3. Làm thế nào để chứng minh một phương trình có nghiệm bằng cách sử dụng tính liên tục?

Bạn cần tìm một hàm số liên tục f(x) sao cho f(a) * f(b) < 0, khi đó phương trình f(x) = 0 có ít nhất một nghiệm thuộc khoảng (a; b).

4. Tại sao tính liên tục lại quan trọng trong toán học và các ứng dụng thực tế?

Tính liên tục cho phép chúng ta dự đoán và mô phỏng các hiện tượng một cách chính xác, đồng thời đảm bảo tính ổn định và an toàn của các hệ thống và công trình.

5. Có những loại gián đoạn nào của hàm số?

Có ba loại gián đoạn chính: gián đoạn bỏ được, gián đoạn bước nhảy, và gián đoạn vô cùng.

6. Làm thế nào để xét tính liên tục của hàm số cho bởi nhiều công thức?

Bạn cần kiểm tra tính liên tục trên từng khoảng mà hàm số được định nghĩa bởi một công thức duy nhất, và kiểm tra tại các điểm chuyển tiếp.

7. Tính liên tục có liên quan gì đến đạo hàm?

Nếu một hàm số có đạo hàm tại một điểm, thì nó liên tục tại điểm đó. Tuy nhiên, điều ngược lại không đúng.

8. Có những hàm số nào không liên tục tại bất kỳ điểm nào?

Có những hàm số như hàm Dirichlet không liên tục tại bất kỳ điểm nào.

9. Làm thế nào để tìm giá trị của tham số để hàm số liên tục?

Bạn cần sử dụng định nghĩa tính liên tục để thiết lập các điều kiện cần thiết và giải phương trình hoặc hệ phương trình để tìm giá trị của tham số.

10. Tính liên tục có ứng dụng gì trong khoa học máy tính?

Tính liên tục được sử dụng trong các thuật toán tối ưu hóa, học máy, và xử lý ảnh.

7. Lời Kết

Hy vọng rằng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về tính liên tục của hàm số. Để nắm vững kiến thức và kỹ năng giải bài tập, hãy luyện tập thường xuyên và tham khảo thêm các nguồn tài liệu khác. tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức!

Đừng quên truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn tự tin chinh phục mọi thử thách trong học tập! Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.