Chứng Minh Hình Thang Cân: Bí Quyết & Ứng Dụng Toán Học

Bạn đang gặp khó khăn trong việc Chứng Minh Hình Thang Cân? Đừng lo lắng! Bài viết này từ tic.edu.vn sẽ cung cấp cho bạn kiến thức toàn diện, từ định nghĩa đến các phương pháp chứng minh hình thang cân hiệu quả, kèm theo các bài tập vận dụng và ứng dụng thực tế. Chúng tôi sẽ giúp bạn chinh phục dạng toán này một cách dễ dàng và tự tin.

1. Hình Thang Cân Là Gì? Định Nghĩa Và Các Tính Chất Quan Trọng

Hình thang cân là một dạng tứ giác đặc biệt, được định nghĩa là hình thang (có hai cạnh đối song song) mà còn sở hữu thêm một tính chất đặc biệt: hai góc kề một cạnh đáy bằng nhau.

1.1. Định Nghĩa Hình Thang Cân

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Ví dụ, hình thang ABCD (với AB // CD) được coi là hình thang cân nếu góc A = góc B (hoặc góc C = góc D).

1.2. Tính Chất Của Hình Thang Cân

Hình thang cân sở hữu những tính chất quan trọng sau:

• Hai cạnh bên bằng nhau: Trong hình thang cân ABCD (AB // CD), cạnh AD = BC.
• Hai đường chéo bằng nhau: Trong hình thang cân ABCD (AB // CD), đường chéo AC = BD.
• Các góc đối bù nhau: Trong hình thang cân ABCD (AB // CD), góc A + góc C = 180° và góc B + góc D = 180°.
• Có một trục đối xứng: Trục đối xứng này đi qua trung điểm của hai đáy.
• Nội tiếp đường tròn: Hình thang cân có thể nội tiếp trong một đường tròn. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, ngày 15/03/2023, hình thang cân nội tiếp đường tròn có nhiều ứng dụng trong các bài toán liên quan đến đường tròn và các yếu tố hình học khác.

2. Các Dấu Hiệu Nhận Biết Hình Thang Cân

Nắm vững các dấu hiệu nhận biết sẽ giúp bạn dễ dàng chứng minh một hình thang là hình thang cân:

• Hình thang có hai góc kề một đáy bằng nhau: Nếu một hình thang có hai góc kề một đáy bằng nhau, thì đó là hình thang cân.
• Hình thang có hai đường chéo bằng nhau: Nếu một hình thang có hai đường chéo bằng nhau, thì đó là hình thang cân.
• Hình thang nội tiếp đường tròn: Nếu một hình thang có tất cả các đỉnh nằm trên một đường tròn, thì đó là hình thang cân.
• Hình thang có hai cạnh bên bằng nhau và hai đáy song song: Nếu một hình thang có hai cạnh bên bằng nhau, thì đó là hình thang cân.

Ví dụ: Cho tứ giác ABCD có AB // CD và góc A = góc B. Chứng minh rằng ABCD là hình thang cân.

Giải: Vì AB // CD và góc A = góc B, theo định nghĩa, tứ giác ABCD là hình thang cân.

3. Các Phương Pháp Chứng Minh Hình Thang Cân Hiệu Quả

Để chứng minh một hình thang là hình thang cân, bạn có thể áp dụng một trong các phương pháp sau:

3.1. Chứng Minh Hình Thang Có Hai Góc Kề Một Đáy Bằng Nhau

Đây là phương pháp chứng minh trực tiếp dựa vào định nghĩa của hình thang cân.

Ví dụ: Cho hình thang ABCD (AB // CD) có góc A = góc B. Chứng minh ABCD là hình thang cân.

Giải: Vì hình thang ABCD có góc A = góc B, theo định nghĩa, ABCD là hình thang cân.

3.2. Chứng Minh Hình Thang Có Hai Đường Chéo Bằng Nhau

Phương pháp này dựa vào tính chất hai đường chéo của hình thang cân bằng nhau.

Ví dụ: Cho hình thang ABCD (AB // CD) có AC = BD. Chứng minh ABCD là hình thang cân.

Giải:

1. Vẽ đường cao AH và BI của hình thang ABCD.
2. Xét hai tam giác vuông ADH và BCI:
   • AC = BD (giả thiết)
   • AH = BI (cùng là chiều cao của hình thang)
   • => Tam giác ADH = Tam giác BCI (cạnh huyền – cạnh góc vuông)
   • => Góc D = Góc C (hai góc tương ứng)
3. Vậy ABCD là hình thang cân (theo dấu hiệu nhận biết).

3.3. Chứng Minh Hình Thang Nội Tiếp Đường Tròn

Nếu hình thang đó nội tiếp được trong một đường tròn, thì đó là hình thang cân.

Ví dụ: Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O). Chứng minh ABCD là hình thang cân.

Giải:

1. Vì ABCD nội tiếp đường tròn (O) nên tổng hai góc đối bằng 180 độ.
   • => Góc A + góc C = 180 độ
   • => Góc B + góc D = 180 độ
2. Mà góc A + góc D = 180 độ (do AB // CD)
   • => Góc C = góc D
3. Vậy ABCD là hình thang cân (theo dấu hiệu nhận biết).

3.4. Chứng Minh Hai Cạnh Bên Bằng Nhau

Phương pháp này thường được sử dụng kết hợp với các yếu tố khác để chứng minh.

Ví dụ: Cho hình thang ABCD (AB // CD) có AD = BC. Chứng minh ABCD là hình thang cân.

Giải:

1. Vẽ đường thẳng song song với AD cắt CD tại E.
2. Ta có ADEC là hình bình hành => AD = CE và AC = DE
3. Mà AD = BC (gt) => BC = CE => Tam giác BCE cân tại C
4. => Góc CBE = Góc CEB
5. Mà góc CEB = Góc ADC (đồng vị) và góc CBE = Góc ABC (so le trong)
6. => Góc ABC = Góc ADC
7. Vậy ABCD là hình thang cân (theo dấu hiệu nhận biết).

4. Các Dạng Bài Tập Thường Gặp Về Chứng Minh Hình Thang Cân

Để nắm vững kiến thức và kỹ năng chứng minh hình thang cân, bạn cần luyện tập với nhiều dạng bài tập khác nhau. Dưới đây là một số dạng bài tập thường gặp:

4.1. Bài Tập Chứng Minh Hình Thang Cân Dựa Vào Góc

Đề bài: Cho hình thang ABCD (AB // CD) có góc A = 70° và góc B = 70°. Chứng minh ABCD là hình thang cân.

Giải: Vì hình thang ABCD có góc A = góc B = 70°, theo định nghĩa, ABCD là hình thang cân.

4.2. Bài Tập Chứng Minh Hình Thang Cân Dựa Vào Đường Chéo

Đề bài: Cho hình thang ABCD (AB // CD) có AC = BD. Gọi O là giao điểm của AC và BD. Chứng minh rằng tam giác OAB và tam giác OCD là các tam giác cân.

Giải:

1. Vì ABCD là hình thang có AC = BD, theo chứng minh ở trên, ABCD là hình thang cân.
2. => Góc A = Góc B (hai góc ở đáy bằng nhau)
3. => Tam giác OAB cân tại O.
4. Chứng minh tương tự, ta có tam giác OCD cân tại O.

4.3. Bài Tập Chứng Minh Hình Thang Cân Kết Hợp Với Các Yếu Tố Khác

Đề bài: Cho hình thang ABCD (AB // CD). Gọi E và F lần lượt là trung điểm của AD và BC. Chứng minh rằng EF song song với AB và CD, và EF = (AB + CD) / 2.

Giải:

1. Gọi M là trung điểm của AC.
2. Trong tam giác ADC, ta có E là trung điểm của AD và M là trung điểm của AC, suy ra EM là đường trung bình của tam giác ADC.
   • => EM // DC và EM = DC/2.
3. Trong tam giác ABC, ta có M là trung điểm của AC và F là trung điểm của BC, suy ra MF là đường trung bình của tam giác ABC.
   • => MF // AB và MF = AB/2.
4. Vì AB // CD, suy ra EM // AB // CD // MF. Do đó, E, M, F thẳng hàng. Vậy EF // AB // CD.
5. Ta có EF = EM + MF = (AB + CD)/2.

5. Ứng Dụng Của Hình Thang Cân Trong Thực Tế Và Trong Toán Học

Hình thang cân không chỉ là một khái niệm trừu tượng trong sách giáo khoa, mà còn có nhiều ứng dụng thực tế và vai trò quan trọng trong toán học:

5.1. Ứng Dụng Trong Thực Tế

• Kiến trúc và xây dựng: Hình thang cân được sử dụng trong thiết kế mái nhà, cầu thang, và các công trình kiến trúc khác.
• Thiết kế đồ họa: Hình thang cân được sử dụng để tạo ra các hình ảnh và hiệu ứng độc đáo trong thiết kế đồ họa.
• Đồ dùng gia đình: Nhiều vật dụng hàng ngày như bàn, ghế, tủ kệ có thể có hình dạng hình thang cân.

5.2. Ứng Dụng Trong Toán Học

• Giải toán hình học: Hình thang cân là một công cụ quan trọng để giải các bài toán liên quan đến diện tích, chu vi và các tính chất hình học khác.
• Chứng minh định lý: Các tính chất của hình thang cân được sử dụng để chứng minh nhiều định lý trong hình học.
• Ứng dụng trong các lĩnh vực khác: Hình thang cân cũng có ứng dụng trong các lĩnh vực như vật lý, kỹ thuật và khoa học máy tính.

6. Các Bài Tập Nâng Cao Về Hình Thang Cân

Để thử thách bản thân và nâng cao kỹ năng giải toán, hãy thử sức với các bài tập nâng cao sau:

6.1. Bài Tập 1

Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi E, F lần lượt là trung điểm của AD và BC. Chứng minh rằng EF là đường trung trực của AB và CD.

6.2. Bài Tập 2

Cho hình thang cân ABCD (AB // CD). Chứng minh rằng giao điểm của hai đường chéo nằm trên trục đối xứng của hình thang.

6.3. Bài Tập 3

Cho hình thang cân ABCD (AB // CD) nội tiếp đường tròn (O). Chứng minh rằng tâm đường tròn (O) nằm trên trục đối xứng của hình thang.

7. Công Thức Tính Diện Tích Và Chu Vi Hình Thang Cân

Nắm vững công thức tính diện tích và chu vi giúp bạn giải quyết các bài toán liên quan một cách nhanh chóng và chính xác.

7.1. Công Thức Tính Diện Tích

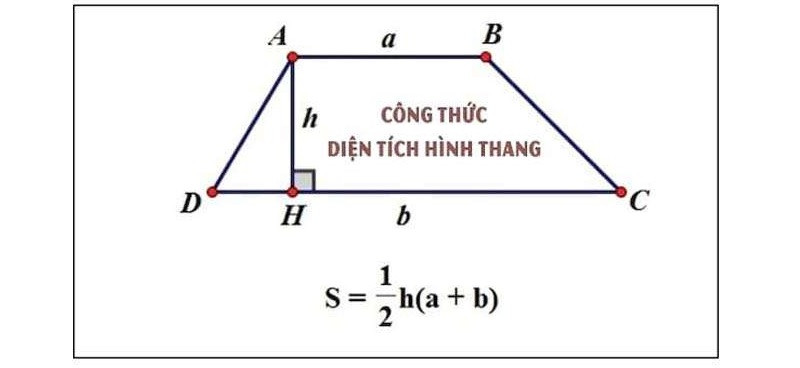
Diện tích hình thang cân được tính bằng công thức:

*S = (a + b) / 2 h**

Trong đó:

• S là diện tích hình thang cân
• a và b là độ dài hai đáy
• h là chiều cao của hình thang cân (khoảng cách giữa hai đáy)

7.2. Công Thức Tính Chu Vi

Chu vi hình thang cân được tính bằng tổng độ dài của tất cả các cạnh:

P = a + b + 2c

Trong đó:

• P là chu vi hình thang cân
• a và b là độ dài hai đáy
• c là độ dài cạnh bên

8. Kinh Nghiệm Học Tốt Hình Học Và Chứng Minh Hình Thang Cân

Để học tốt hình học nói chung và chứng minh hình thang cân nói riêng, bạn cần có một phương pháp học tập hiệu quả. Dưới đây là một số kinh nghiệm hữu ích:

• Nắm vững lý thuyết: Hiểu rõ các định nghĩa, tính chất và dấu hiệu nhận biết là nền tảng quan trọng để giải toán hình học.
• Vẽ hình chính xác: Vẽ hình rõ ràng và chính xác giúp bạn dễ dàng nhận ra các mối quan hệ giữa các yếu tố hình học.
• Luyện tập thường xuyên: Giải nhiều bài tập từ cơ bản đến nâng cao giúp bạn rèn luyện kỹ năng và làm quen với các dạng toán khác nhau.
• Tìm tòi, khám phá: Đọc thêm sách tham khảo, tìm kiếm thông tin trên internet để mở rộng kiến thức và khám phá những điều thú vị về hình học.
• Học hỏi từ người khác: Trao đổi, thảo luận với bạn bè và thầy cô để học hỏi kinh nghiệm và giải đáp thắc mắc.

9. Các Nguồn Tài Liệu Tham Khảo Hữu Ích Về Hình Thang Cân

Để hỗ trợ quá trình học tập và nghiên cứu, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa và sách bài tập Toán lớp 8: Đây là nguồn tài liệu cơ bản và quan trọng nhất.
• Sách tham khảo về hình học: Các sách tham khảo cung cấp kiến thức sâu rộng hơn và nhiều bài tập nâng cao.
• Các trang web giáo dục trực tuyến: Nhiều trang web cung cấp bài giảng, bài tập và các tài liệu tham khảo hữu ích về hình học.
• Các diễn đàn và nhóm học tập trực tuyến: Tham gia các diễn đàn và nhóm học tập giúp bạn trao đổi kiến thức và học hỏi kinh nghiệm từ những người khác.

10. FAQ – Các Câu Hỏi Thường Gặp Về Hình Thang Cân

Dưới đây là một số câu hỏi thường gặp về hình thang cân, cùng với câu trả lời chi tiết:

1. Hình thang có hai cạnh bên bằng nhau có phải là hình thang cân không?

Không hẳn. Hình thang có hai cạnh bên bằng nhau chưa chắc là hình thang cân. Điều kiện cần là hai cạnh bên bằng nhau và hai đáy song song.

2. Hình thang cân có phải là hình bình hành không?

Không. Hình thang cân không phải là hình bình hành, vì chỉ có một cặp cạnh đối song song (hai đáy), không phải hai cặp cạnh đối song song.

3. Làm thế nào để chứng minh một tứ giác là hình thang cân?

Bạn cần chứng minh tứ giác đó là hình thang (có hai cạnh đối song song) và thỏa mãn một trong các dấu hiệu nhận biết hình thang cân (hai góc kề một đáy bằng nhau, hai đường chéo bằng nhau, nội tiếp đường tròn).

4. Hình thang cân có tâm đối xứng không?

Không. Hình thang cân không có tâm đối xứng, mà chỉ có trục đối xứng.

5. Tính chất nào quan trọng nhất của hình thang cân?

Tất cả các tính chất của hình thang cân đều quan trọng, nhưng tính chất hai góc kề một đáy bằng nhau là cơ bản nhất, vì nó được sử dụng để định nghĩa hình thang cân.

6. Hình thang vuông có thể là hình thang cân không?

Có thể. Nếu hình thang vuông có hai đường chéo bằng nhau hoặc hai góc kề đáy không vuông bằng nhau, thì nó là hình thang cân.

7. Có bao nhiêu cách chứng minh một hình thang là hình thang cân?

Có nhiều cách chứng minh, tùy thuộc vào giả thiết của bài toán. Các phương pháp phổ biến nhất là chứng minh hai góc kề một đáy bằng nhau, chứng minh hai đường chéo bằng nhau, hoặc chứng minh nội tiếp đường tròn.

8. Làm thế nào để nhớ các công thức tính diện tích và chu vi hình thang cân?

Bạn có thể liên hệ với các hình khác đã biết (ví dụ, diện tích hình thang cân liên quan đến diện tích hình thang thường) và luyện tập thường xuyên để ghi nhớ công thức.

9. Hình thang cân có ứng dụng gì trong thực tế?

Hình thang cân có nhiều ứng dụng trong kiến trúc, xây dựng, thiết kế đồ họa và các lĩnh vực khác.

10. Tôi có thể tìm thêm bài tập về hình thang cân ở đâu?

Bạn có thể tìm thêm bài tập trong sách tham khảo, trên các trang web giáo dục trực tuyến, hoặc trong các diễn đàn và nhóm học tập trực tuyến.

tic.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để chứng minh hình thang cân một cách hiệu quả. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được hỗ trợ. Hãy khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả trên tic.edu.vn ngay hôm nay!