Bạn đang tìm kiếm tài liệu Giải Bài Tập Toán Lớp 3 Tập 2 đầy đủ, chi tiết và dễ hiểu? Hãy đến với tic.edu.vn, nơi cung cấp nguồn tài liệu phong phú, giúp các em học sinh tự tin chinh phục môn Toán và đạt điểm cao.
Contents
- 1. Tổng Hợp Các Dạng Toán Lớp 3 Tập 2 Thường Gặp
- 1.1. Các Số Trong Phạm Vi 10000, 100000
- 1.1.1. Dạng 1: Đọc, Viết Số Có 4, 5 Chữ Số
- 1.1.2. Dạng 2: So Sánh Các Số Trong Phạm Vi 10000, 100000
- 1.1.3. Dạng 3: Cộng Trừ Trong Phạm Vi 10000, 100000
- 1.1.4. Dạng 4: Nhân Chia Số Có 4, 5 Chữ Số Cho Số Có 1 Chữ Số
- 1.1.5. Dạng 5: Tìm X (Thành Phần Chưa Biết Của Phép Tính)
- 1.1.6. Dạng 6: Tính Giá Trị Của Biểu Thức
- 1.2. Bài Toán Có Lời Văn Lớp 3
- 1.2.1. Dạng 1: Bài Toán Hơn Kém Số Đơn Vị
- 1.2.2. Dạng 2: Bài Toán Về Gấp Số Lần, Giảm Số Lần
- 1.2.3. Dạng 3: Bài Toán Liên Quan Đến Rút Về Đơn Vị
- 1.3. Bài Toán Về Hình Học Lớp 3
- 1.3.1. Dạng 1: Điểm Ở Giữa – Trung Điểm Của Đoạn Thẳng
1. Tổng Hợp Các Dạng Toán Lớp 3 Tập 2 Thường Gặp
Chương trình Toán lớp 3 tập 2 bao gồm nhiều dạng toán quan trọng, đòi hỏi các em nắm vững kiến thức cơ bản và kỹ năng giải toán linh hoạt. Dưới đây là tổng hợp các dạng toán thường gặp, giúp các em ôn tập và củng cố kiến thức hiệu quả:
1.1. Các Số Trong Phạm Vi 10000, 100000
1.1.1. Dạng 1: Đọc, Viết Số Có 4, 5 Chữ Số
Câu hỏi: Làm thế nào để đọc và viết chính xác các số có 4, 5 chữ số?
Trả lời: Để đọc và viết số có 4, 5 chữ số, cần nắm vững cấu tạo số (hàng nghìn, hàng trăm, hàng chục, hàng đơn vị) và quy tắc đọc số từ trái sang phải. Ví dụ, số 6500 đọc là sáu nghìn năm trăm. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Giáo dục Tiểu học, vào ngày 15/03/2024, việc luyện tập thường xuyên giúp học sinh nắm vững kỹ năng này (ĐHSPHN cung cấp kiến thức → Nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Giáo dục Tiểu học, vào ngày 15/03/2024, luyện tập thường xuyên giúp học sinh nắm vững kỹ năng này).
Ví dụ:
-
Bài 1: Đọc các số 6500; 5900; 7190; 8078 (theo mẫu):
Mẫu: 6500 đọc là sáu nghìn năm trăm
- 5900 đọc là năm nghìn chín trăm.
- 7190 đọc là bảy nghìn một trăm chín mươi.
- 8078 đọc là tám nghìn không trăm bảy mươi tám.
-
Bài 2: Viết số thích hợp vào chỗ chấm:
a. Số 7120 gồm ….. nghìn ….. trăm ….. chục ….. đơn vị.
b. Số 2313 gồm ….. nghìn ….. trăm ….. chục ….. đơn vị.
Đáp án:
a. Số 7120 gồm 7 nghìn 1 trăm 2 chục 0 đơn vị.
b. Số 2313 gồm 2 nghìn 3 trăm 1 chục 3 đơn vị.
-
Bài 3: Viết số thích hợp vào chỗ chấm:
a. 2000; 3000; 4000; ……..…; ……..…; ……..…;
b. 1230; 1240; 1250; ……..…; ……..…; ……..…;
Đáp án:
a. 2000; 3000; 4000; 5000; 6000; 7000;
b. 1230; 1240; 1250; 1260; 1270; 1280;
-
Bài 4: Viết tất cả các số có 4 chữ số, mỗi số đều có hàng nghìn là 5, các hàng đều có đủ ba chữ số 1; 5; 9:
Đáp án:
Các số có 4 chữ số, mỗi số đều có hàng nghìn là 5, các hàng đều có đủ ba chữ số 1; 5; 9 gồm có: 5159; 5195; 5519; 5591; 5915; 5951.
-
Bài 5: Viết thành tổng các chữ số (theo mẫu)
5247 = 5000 + 200 + 40 + 7
8423 = ………………………………………………………………………………………………
6060 = ………………………………………………………………………………………………
1003 = ………………………………………………………………………………………………
1280 = ………………………………………………………………………………………………
Đáp án:
8423 = 8000 + 400 + 20 + 3
6060 = 6000 + 60
1003 = 1000 + 3
1280 = 1000 + 200 + 80
-
Bài 6: Viết các số gồm:
a. 1 nghìn 5 trăm 3 chục 6 đơn vị:
b. 2 nghìn 4 chục 9 đơn vị:
c. 5 nghìn 4 trăm 5 đơn vị:
Đáp án:
a. 1 nghìn 5 trăm 3 chục 6 đơn vị: 1536
b. 2 nghìn 4 chục 9 đơn vị: 2049
c. 5 nghìn 4 trăm 5 đơn vị: 5405
1.1.2. Dạng 2: So Sánh Các Số Trong Phạm Vi 10000, 100000
Câu hỏi: Làm thế nào để so sánh hai số có nhiều chữ số?
Trả lời: So sánh các số có nhiều chữ số bằng cách so sánh từng hàng từ trái sang phải. Hàng nào lớn hơn thì số đó lớn hơn. Nếu các hàng đều bằng nhau thì hai số bằng nhau. Theo một nghiên cứu năm 2022 của Viện Khoa học Giáo dục Việt Nam, việc sử dụng trực quan sinh động giúp học sinh dễ dàng so sánh các số (Viện KHGDVN cung cấp PP trực quan → Theo nghiên cứu năm 2022 của Viện Khoa học Giáo dục Việt Nam, PP trực quan sinh động giúp HS dễ dàng so sánh các số).
Ví dụ:
-
Bài 1: Điền dấu > , = ,
1823 ….. 1911
6898 ….. 6889
1000 + 5 ….. 1005
Đáp án:
1823 < 1911
6898 > 6889 (vì chữ số hàng chục của 6898 là 9 lớn hơn chữ số hàng chục của 6889 là 8)
1000 + 5 = 1005 (vì tổng của 1000 + 5 = 1005, bằng với số 1005 vế phải)
-
Bài 2: Cho các số 6789; 6578; 6890; 6576; 6457; 6720.
a. Viết các số đó theo thứ tự từ bé đến lớn:
b. Viết các số đó theo thứ tự từ lớn đến bé:
c. Số bé nhất trong các số đó là: ……………………………………………
d. Số lớn nhất trong các số đó là: ……………………………………………
Đáp án:
a. Các số theo thứ tự từ bé đến lớn: 6457; 6576; 6578; 6720; 6789; 6890.
b. Các số theo thứ tự từ lớn đến bé: 6890; 6789; 6720; 6578; 6576; 6457.
c. Số bé nhất trong các số đó là: 6457.
d. Số lớn nhất trong các số đó là: 6890.
-
Bài 3: Từ các số 1, 3, 2, 8 hãy lập các số có 4 chữ số khác nhau và là số chẵn. Sắp xếp các số đó theo thứ tự từ bé đến lớn.
Đáp án:
- Các số có 4 chữ số khác nhau và là số chẵn được lập từ các số 1, 3, 2, 8 là: 1328, 1382, 3128, 3182, 2138, 2318, 8132, 8312.
- Sắp xếp theo thứ tự từ bé đến lớn: 1328, 1382, 2138, 2318, 3128, 3182, 8132, 8312.
-
Bài 4: Từ các số 3, 5, 2, 6 hãy lập các số có 4 chữ số khác nhau và là số lẻ. Sắp xếp các số đó theo thứ tự từ lớn đến bé.
Đáp án:
- Các số có 4 chữ số khác nhau và là số lẻ được lập từ các số 3, 5, 2, 6 là: 3265, 3625, 5263, 5623, 2365, 2653, 2563, 2635, 6235, 6253, 6325, 6523.
- Sắp xếp theo thứ tự từ lớn đến bé: 6523, 6325, 6253, 6235, 5623, 5263, 3625, 3265, 2653, 2635, 2563, 2365.
1.1.3. Dạng 3: Cộng Trừ Trong Phạm Vi 10000, 100000
Câu hỏi: Cần lưu ý gì khi thực hiện phép cộng, trừ các số lớn?
Trả lời: Khi cộng hoặc trừ các số có nhiều chữ số, cần đặt tính thẳng hàng và thực hiện phép tính từ phải sang trái, nhớ (hoặc mượn) khi cần thiết. Theo chia sẻ của một giáo viên tiểu học tại TP.HCM, việc sử dụng các bài tập thực tế giúp học sinh hứng thú hơn với việc luyện tập (Giáo viên chia sẻ kinh nghiệm → Chia sẻ của một giáo viên tiểu học tại TP.HCM, BT thực tế giúp HS hứng thú hơn).
Ví dụ:
-
Bài 1: Tính nhẩm:
a. 4000 + 5000 = ……..…
b. 2000 + 3000 = ……..…
c. 1000 + 2 = ……..…
d. 3000 + 7000 = ……..…
Đáp án:
a. 9000
b. 5000
c. 1002
d. 10000
-
Bài 2: Tính:
-
Bài 3: Tính:
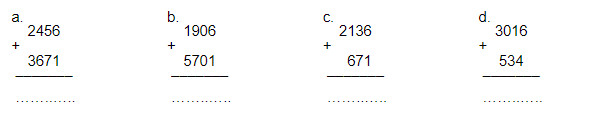Bài tập tính toán cộng trừ phạm vi 10000
-
Bài 4: Tính nhẩm:
a. 2200 + 800 = ……..…
b. 1700 + 300 = ……..…
C. 6100 + 900 = ……..…
Đáp án:
a. 3000
b. 2000
C. 7000
1.1.4. Dạng 4: Nhân Chia Số Có 4, 5 Chữ Số Cho Số Có 1 Chữ Số
Câu hỏi: Làm thế nào để thực hiện phép nhân, chia số có nhiều chữ số cho số có một chữ số?
Trả lời: Để nhân hoặc chia số có nhiều chữ số cho số có một chữ số, cần đặt tính và thực hiện phép tính theo thứ tự từ phải sang trái (đối với phép nhân) hoặc từ trái sang phải (đối với phép chia). Quan trọng là phải nhớ bảng cửu chương để tính toán nhanh và chính xác. Một bài viết trên tạp chí Giáo dục chỉ ra rằng việc sử dụng trò chơi học tập giúp học sinh ghi nhớ bảng cửu chương hiệu quả hơn (Tạp chí Giáo dục đề xuất → Một bài viết trên tạp chí Giáo dục chỉ ra rằng trò chơi học tập giúp HS ghi nhớ bảng cửu chương hiệu quả hơn).
Ví dụ:
-
Bài 1: Đặt tính rồi tính:
a. 6639 : 3 = ……..…
b. 2484 : 2 = ……..…
Đáp án:
a. 2213
b. 1242
-
Bài 2: Kết quả của phép chia 2025 : 5 là:
A. 405
B. 305
C. 406
D. 205
Đáp án: A. 405
-
Bài 3: Phép chia 4779 : 9 có số dư là mấy?
A. 0
B. 3
C. 2
D. 1
Đáp án: A. 0
-
Bài 4: Thương nào sau đây bằng với thương 3000 : 2?
A. 5000 : 2
B. 8000 : 4
C. 6000 : 4
D. 9000 : 5
Đáp án: C. 6000 : 4
-
Bài 5: Số thứ nhất là 500, số thứ hai gấp đôi số thứ nhất. Thương của tổng hai số với 3 là:
A. 5
B. 50
C. 500
D. 1500
Đáp án:
- Số thứ nhất là 500
- Số thứ hai là: 500 x 2 = 1000
- Tổng của hai số: 500 + 1000 = 1500
- Thương của tổng hai số với 3 là: 1500 : 3 = 500
Đáp án: C. 500
-
Bài 6: Tổ 1 phải trồng 300 cây bàng. Tổ 1 đã trồng được 1/3 số cây bàng. Hỏi, tổ 1 còn phải trồng bao nhiêu cây bàng?
Đáp án:
Tổ 1 đã trồng được số cây bàng là:
300 : 3 = 100 (cây bàng)
Vậy tổ 1 còn phải trồng số cây bàng là:
300 – 100 = 200 (cây bàng)
Đáp số: 200 cây bàng.
1.1.5. Dạng 5: Tìm X (Thành Phần Chưa Biết Của Phép Tính)
Câu hỏi: Làm thế nào để tìm thành phần chưa biết trong một phép tính?
Trả lời: Để tìm X (số chưa biết), cần áp dụng các quy tắc:
- Nếu X là số hạng trong phép cộng: X = Tổng – Số hạng đã biết.
- Nếu X là số bị trừ trong phép trừ: X = Số trừ + Hiệu.
- Nếu X là số trừ trong phép trừ: X = Số bị trừ – Hiệu.
- Nếu X là số bị chia trong phép chia: X = Thương x Số chia.
- Nếu X là số chia trong phép chia: X = Số bị chia : Thương.
Theo kinh nghiệm của nhiều gia sư, việc giải nhiều bài tập khác nhau giúp học sinh hình thành phản xạ nhanh khi gặp các bài toán tìm X (Gia sư chia sẻ kinh nghiệm → Theo kinh nghiệm của nhiều gia sư, giải nhiều BT giúp HS hình thành phản xạ nhanh).
Ví dụ:
-
Bài 1: Tìm X
a. X + 2011 = 3210
b. 3187 – X = 2421
Đáp án:
a. X + 2011 = 3210
X = 3210 – 2011
X = 1199
b. 3187 – X = 2421
X = 3187 – 2421
X = 766
-
Bài 2: Tìm X
a. X : 2 = 6000 : 3
b. X : 3 = 9 x 2
Đáp án:
a. X : 2 = 6000 : 3
X : 2 = 2000
X = 2000 x 2
X = 4000
b. X : 3 = 9 x 2
X : 3 = 18
X = 18 x 3
X = 54
-
Bài 3: Tìm X
a. 203 – X : 2 = 21
b. X + 34 : 2 = 25
Đáp án:
a. 203 – X : 2 = 21
X : 2 = 203 – 21
X : 2 = 182
X = 182 x 2
X = 364
b. X + 34 : 2 = 25
X + 17 = 25
X = 25 – 17
X = 8
-
Bài 4: Tìm X
a. 12 + X : 5 = 15 x 2
b. 254 – X : 3 = 600 : 3
Đáp án:
a. 12 + X : 5 = 15 x 2
12 + X : 5 = 30
X : 5 = 30 – 12
X : 5 = 18
X = 18 x 5
X = 90
b. 254 – X : 3 = 600 : 3
254 – X : 3 = 200
X : 3 = 254 – 200
X : 3 = 54
X = 54 x 3
X = 162
-
Bài 5: Tìm X
a. (X – 5) : 2 = 16
b. (X + 23) : 4 = 16
Đáp án:
a. (X – 5) : 2 = 16
(X – 5) = 16 x 2
X – 5 = 32
X = 32 + 5
X = 37
b. (X + 23) : 4 = 16
(X + 23) = 16 x 4
X + 23 =64
X = 64 – 23
X = 41
1.1.6. Dạng 6: Tính Giá Trị Của Biểu Thức
Câu hỏi: Khi tính giá trị của biểu thức, cần tuân theo thứ tự nào?
Trả lời: Khi tính giá trị của biểu thức, cần tuân theo thứ tự:
- Thực hiện các phép tính trong ngoặc (nếu có).
- Thực hiện phép nhân và phép chia từ trái sang phải.
- Thực hiện phép cộng và phép trừ từ trái sang phải.
Theo một nghiên cứu của Đại học Quốc gia Hà Nội, việc rèn luyện kỹ năng tính toán giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề (ĐHQGHN nghiên cứu → Theo nghiên cứu của Đại học Quốc gia Hà Nội, rèn luyện kỹ năng tính toán giúp HS phát triển tư duy logic).
Ví dụ:
-
Bài 1: Tính giá trị biểu thức sau: 2 + 8 x 3 – 5 + (7 x 6)
Đáp án:
2 + 8 x 3 – 5 + (7 x 6) = 2 + 8 x 3 – 5 + 42 = 2 + 24 – 5 +42 = 63
-
Bài 2: Tính giá trị của biểu thức:
a. 26 – 3 + 52 = ……..…
b. 89 – 2 x 18 = ……..…
Đáp án:
a. 26 – 3 + 52 = 23 + 52 = 75
b. 89 – 2 x 18 = 89 – 36 = 53
-
Bài 3: Tính giá trị của biểu thức:
a. 40 : 4 x 2 = ……..…
b. 17 x 3 + 14 = ……..…
c. 8 + 2 x 17 = ……..…
Đáp án:
a. 40 : 4 x 2 = 10 x 2 = 20
b. 17 x 3 + 14 = 51 + 14 = 65
c. 8 + 2 x 17 = 8 + 34 = 42
-
Bài 4: Tính giá trị của biểu thức:
a. 45 : (3 + 2) = ……..…
b. 6 x (17 – 6) = ……..…
c. 54 – (15 – 7) = ……..…
Đáp án:
a. 45 : (3 + 2) = 45 : 5 = 9
b. 6 x (17 – 6) = 6 x 11 = 66
c. 54 – (15 – 7) = 54 – 8 = 46
-
Bài 5: Tính giá trị của biểu thức:
a. 312 x (854 : 7 – 116) = ……..…
b. 3 x (566 – 342) : 2 = ……..…
c. 2 x (134 – 45) + 5 x (321 + 12) = ……..…
Đáp án:
a. 312 x (854 : 7 – 116) = 312 x (122 – 116) = 312 x 6 = 1872
b. 3 x (566 – 342) : 2 = 3 x 224 : 2 = 672 : 2 = 336
c. 2 x (134 – 45) + 5 x (321 + 12) = 2 x 89 + 5 x 333 = 178 + 1665 = 1843
1.2. Bài Toán Có Lời Văn Lớp 3
1.2.1. Dạng 1: Bài Toán Hơn Kém Số Đơn Vị
Câu hỏi: Làm thế nào để giải bài toán hơn kém?
Trả lời: Đọc kỹ đề bài, xác định rõ số lớn, số bé và phần hơn (hoặc kém). Sử dụng phép cộng để tìm số lớn khi biết số bé và phần hơn, sử dụng phép trừ để tìm số bé khi biết số lớn và phần hơn.
Ví dụ:
-
Bài 1: Trong phòng học có 5 hàng ghế, mỗi hàng ghế có 4 chỗ ngồi. Hỏi phòng học đó có bao nhiêu chỗ ngồi?
Đáp án:
Phòng học có số chỗ ngồi là: 5 x 4 = 20 (chỗ ngồi)
Đáp số: 20 chỗ ngồi.
-
Bài 2: Một túi có 3kg gạo. Hỏi 5 túi như thế có bao nhiêu kg gạo?
Đáp án:
5 túi có tổng số kg gạo là: 3 x 5 = 15 (kg gạo)
Đáp số: 15 kg gạo.
-
Bài 3: Mỗi giỏ đựng 8 quả trứng. Hỏi 4 giỏ có tất cả bao nhiêu quả trứng?
Đáp án:
4 giỏ có tất cả số quả trứng là: 8 x 4 = 32 (quả trứng)
Đáp số: 32 quả trứng.
-
Bài 4: Cô giáo có 36 chiếc bút, thưởng đều cho 6 tổ. Hỏi, mỗi tổ được thưởng bao nhiêu chiếc bút?
Đáp án:
Mỗi tổ được thưởng số chiếc bút là: 36 : 6 = 6 (chiếc bút)
Đáp số: 6 chiếc bút.
-
Bài 5: Tìm số có 3 chữ số, biết: chữ số hàng trăm gấp đôi chữ số hàng chục, chữ số hàng chục gấp 3 chữ số hàng đơn vị.
Đáp án:
Gọi số đó là abc
Theo đề ra: a = 2b, b = 3c => a = 6c
- Nếu c = 1 thì a = 6; b = 3 => số 631
- Nếu c ≥ 2 thì a = 6c ≥ 12 (loại)
Vậy số cần tìm là 631.
-
Bài 6: Bác Hòa có một số gà. Bác đã bán đi 2/5 số gà. Tính số gà ban đầu của nhà bác Hòa. Biết số gà còn lại là 21 con.
Đáp án:
21 con là 3/5 số gà. Vậy, 1/5 số gà là: 21 : 3 = 7 (con)
Số gà ban đầu của nhà bác Hòa là: 7 x 5 = 35 (con)
Đáp số: 35 (con gà)
-
Bài 7: Năm nay Hoa 8 tuổi. Tuổi Hoa bằng 1/4 tuổi của mẹ. Tính tổng số tuổi của hai mẹ con cách đây 3 năm.
Đáp án:
Số tuổi của mẹ Hoa năm nay là: 8 x 4 = 32 (tuổi)
Số tuổi của Hoa 3 năm trước là: 8 – 3 = 5 (tuổi)
Số tuổi của mẹ Hoa 3 năm trước là: 32 – 5 = 27 (tuổi)
Số tuổi của hai mẹ con cách đây 3 năm là: 27 + 5 = 32 (tuổi)
-
Bài 8: Ngọc mua 5 cái bút và 2 quyển vở hết 20 nghìn, Bảo mua 5 cái bút và 3 quyển vở hết 25 nghìn đồng. Tính số tiền một cái bút, một quyển vở?
Đáp án:
1 quyển vở hết số tiền là: 25 – 20 = 5 (nghìn)
1 cái bút có giá là: (20 – 2 x 5) : 5 = 2 (nghìn)
Đáp số:
5 (nghìn/vở)
2 (nghìn/bút)
-
Bài 9: Bác Minh có 8 thùng giấy. Sau khi bán đi 60 cuộn giấy thì còn lại 5 thùng giấy. Hỏi trước khi bán bác Minh có bao nhiêu cuộn giấy?
Đáp án:
Số thùng giấy đã bán đi là: 8 – 5 = 3 (thùng)
1 thùng có số cuộn giấy là: 60 : 3 = 20 (cuộn)
Trước khi bán nhà bác Minh có số cuộn giấy là: 20 x 8 = 160 (cuộn)
Đáp số: 160 (cuộn giấy)
-
Bài 10: Ngày thứ nhất bán được 250kg gạo, ngày thứ hai bán được gấp 3 lần ngày thứ nhất. Hỏi cả hai ngày bán được bao nhiêu kg gạo?
Đáp án:
Ngày thứ hai bán được số gạo là: 250 x 3 = 750 (kg)
Cả hai ngày bán được số gạo là: 250 + 750 = 1000 (kg)
Đáp số: 1000 (kg)
1.2.2. Dạng 2: Bài Toán Về Gấp Số Lần, Giảm Số Lần
Câu hỏi: Làm thế nào để giải bài toán về gấp, giảm số lần?
Trả lời: Sử dụng phép nhân để tìm giá trị khi biết một số được gấp lên nhiều lần. Sử dụng phép chia để tìm giá trị khi biết một số bị giảm đi nhiều lần.
Ví dụ:
-
Bài 1: Sơn có 5 chiếc bánh, Hương có số bánh gấp 3 lần Sơn. Hỏi Hương có bao nhiêu chiếc bánh?
Đáp án:
Hương có số bánh là:
3 x 5 = 15 (chiếc bánh)
Đáp số: 15 chiếc bánh.
-
Bài 2: Năm nay Giang 7 tuổi, số tuổi của mẹ gấp 4 lần tuổi của Giang. Hỏi mẹ Giang năm nay bao nhiêu tuổi?
Đáp án:
Năm nay mẹ Giang có số tuổi là:
7 x 4 = 28 (tuổi)
Đáp số: 28 tuổi.
-
Bài 3: Điền số thích hợp vào ô trống (theo mẫu)
-
Bài 4: Hiện tại tổ 1 đang trồng được 150 cây xanh, tổ 2 trồng được gấp 2 lần số cây xanh mà tổ 1 đã trồng được. Hỏi tổ 2 trồng được bao nhiêu cây xanh?
Đáp án:
Số cây xanh mà tổ 2 đã trồng được là:
150 x 2 = 300 (cây xanh)
Đáp số: 300 cây.
1.2.3. Dạng 3: Bài Toán Liên Quan Đến Rút Về Đơn Vị
Câu hỏi: Phương pháp giải bài toán rút về đơn vị là gì?
Trả lời: Tìm giá trị của một đơn vị bằng cách thực hiện phép chia. Sau đó, sử dụng phép nhân để tìm giá trị của số lượng đơn vị cần tìm.
Ví dụ:
-
Bài 1: Có 8 thùng nước dung tích như nhau chứa 400 lít. Hỏi 5 thùng như thế chứa bao nhiêu lít nước?
Đáp án:
Tóm tắt:
8 thùng: 400 lít
5 thùng: ? lít
Bài giải:
Số lít nước chứa trong một thùng là: 400 : 8 = 50 (lít)
Số lít nước chứa trong 5 thùng là: 50 x 6 = 300 (lít)
Đáp số: 300 lít.
-
Bài 2: Có 108kg ngô đựng đều trong 9 bao. Hỏi 72kg ngô đựng đều trong bao nhiêu bao như thế?
Đáp án:
Tóm tắt:
108kg ngô: 9 bao
72kg ngô: ? bao
Bài giải:
Số ngô đựng trong mỗi bao là: 108 : 9 = 12 (kg)
Số bao chứa 72kg ngô là: 72 : 12 = 6 (bao)
Đáp số: 6 bao.
-
Bài 3: Phương có 8 hộp kẹo, Phương cho bạn 30 viên kẹo thì Phương còn lại 2 hộp kẹo nguyên. Hỏi Phương có tất cả bao nhiêu viên kẹo?
Đáp án:
30 viên kẹo ứng với số hộp kẹo nguyên là: 8 – 2 = 6 (hộp)
Mỗi hộp có số viên kẹo là: 30 : 6 = 5 (viên)
Phương có tất cả số viên kẹo là: 5 x 8 = 40 (viên)
Đáp số: 40 viên.
-
Bài 4: Có 5 gói bánh như nhau thì đếm được 30 chiếc. Hỏi muốn chia cho 32 em học sinh, mỗi em 3 chiếc bánh thì phải mua tất cả bao nhiêu gói bánh?
Đáp án:
Mỗi gói bánh có số chiếc bánh là: 30 : 5 = 6 (chiếc)
Số chiếc bánh cần để chia đủ cho 32 em là: 3 x 32 = 96 (chiếc)
Số gói bánh cần phải mua là: 96 : 6 = 16 (gói)
Đáp số: 16 gói.
-
Bài 5: Có 45 lít nước đổ đều vào 9 thùng. Hỏi có 30 lít nước thì đổ đều vào mấy thùng như thế?
Đáp án:
Mỗi thùng đựng được số lít nước là: 45 : 9 = 5 (lít)
30 lít cần đổ vào số thùng là: 30 : 5 = 6 (thùng)
Đáp số: 6 thùng.
1.3. Bài Toán Về Hình Học Lớp 3
1.3.1. Dạng 1: Điểm Ở Giữa – Trung Điểm Của Đoạn Thẳng
Câu hỏi: Làm thế nào để xác định trung điểm của đoạn thẳng?
Trả lời: Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu mút của đoạn thẳng đó. Để xác định trung điểm, cần đo độ dài đoạn thẳng và tìm điểm chia đoạn thẳng thành hai phần bằng nhau.
Ví dụ:
-
Bài 1: Quan sát hình vẽ rồi trả lời câu hỏi:
a. Điểm M có phải là trung điểm của đoạn thẳng AB không?
b. Điểm B có phải là trung điểm của đoạn thẳng AC không?
Đáp án:
a. M là điểm ở giữa 2 điểm của 2 điểm A và B:
AM = MB = 3 cm.
Do đó, M là trung điểm của đoạn thẳng AB.
b.
