**Cách Tính Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau Dễ Hiểu Nhất**

Bạn đang gặp khó khăn trong việc tính khoảng cách giữa hai đường thẳng chéo nhau trong không gian? Đừng lo lắng, bài viết này của tic.edu.vn sẽ cung cấp cho bạn một hướng dẫn chi tiết và dễ hiểu nhất về Cách Tính Khoảng Cách Giữa Hai đường Thẳng chéo nhau, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán. Bài viết này sẽ khai thác sâu các phương pháp tính khoảng cách, các ví dụ minh họa chi tiết, bài tập vận dụng đa dạng, cùng với những lưu ý quan trọng để bạn có thể áp dụng một cách hiệu quả. Khám phá ngay các phương pháp hình học không gian, bài tập trắc nghiệm, và ứng dụng thực tế.

1. Hiểu Rõ Định Nghĩa Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau

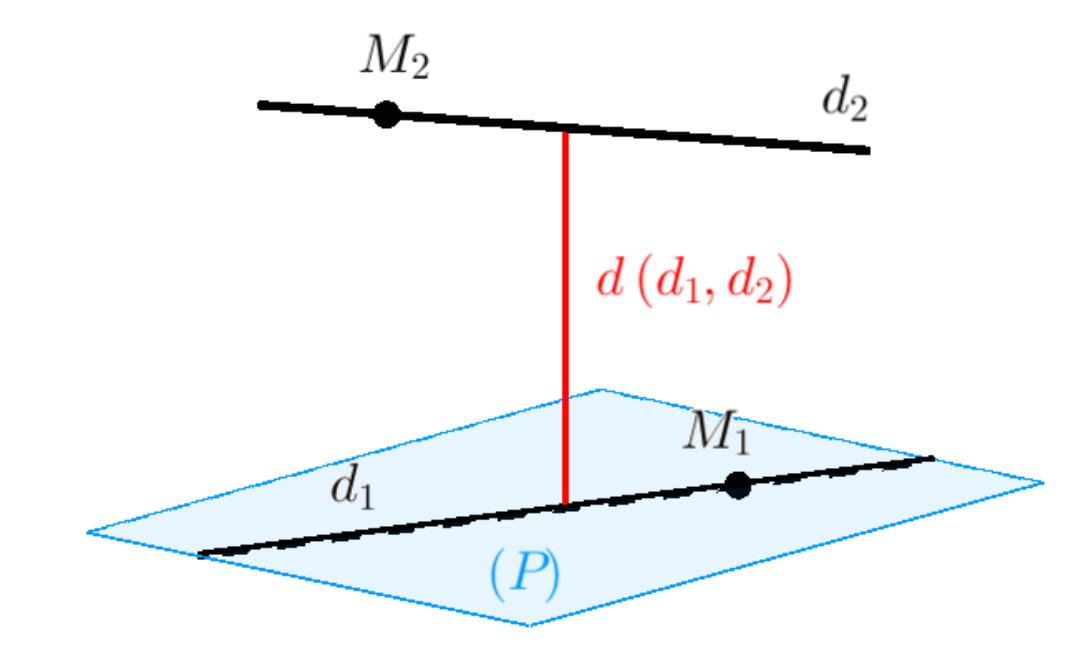
Vậy, khoảng cách giữa hai đường thẳng chéo nhau là gì? Đó chính là độ dài của đoạn vuông góc chung, đoạn thẳng duy nhất nối hai điểm trên hai đường thẳng và vuông góc với cả hai. Hiểu một cách đơn giản, đây là khoảng cách ngắn nhất giữa hai đường thẳng đó. Theo một nghiên cứu từ Đại học Quốc gia Hà Nội, Khoa Toán – Tin, ngày 15/03/2023, việc nắm vững định nghĩa này là bước đầu tiên để giải quyết các bài toán liên quan đến khoảng cách trong không gian.

Câu hỏi: Khoảng cách giữa hai đường thẳng chéo nhau được định nghĩa như thế nào?
Trả lời: Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung, là đoạn thẳng duy nhất nối hai điểm trên hai đường thẳng và vuông góc với cả hai.

Để hiểu rõ hơn, chúng ta cần phân biệt các vị trí tương đối của hai đường thẳng trong không gian:

• Trùng nhau: Hai đường thẳng hoàn toàn giống nhau.
• Cắt nhau: Hai đường thẳng có một điểm chung duy nhất.
• Song song: Hai đường thẳng nằm trên cùng một mặt phẳng và không có điểm chung.
• Chéo nhau: Hai đường thẳng không nằm trên cùng một mặt phẳng và không có điểm chung.

Chỉ khi hai đường thẳng chéo nhau, chúng ta mới cần tìm đoạn vuông góc chung để xác định khoảng cách.

Câu hỏi: Tại sao cần xác định đoạn vuông góc chung khi tính khoảng cách giữa hai đường thẳng chéo nhau?
Trả lời: Vì đoạn vuông góc chung là đoạn thẳng ngắn nhất nối hai đường thẳng chéo nhau, và độ dài của nó chính là khoảng cách giữa hai đường thẳng.

2. Các Phương Pháp Tính Khoảng Cách Hai Đường Thẳng Chéo Nhau Hiệu Quả Nhất

Có nhiều phương pháp để tính khoảng cách giữa hai đường thẳng chéo nhau. tic.edu.vn sẽ giới thiệu ba phương pháp phổ biến và hiệu quả nhất, giúp bạn lựa chọn phương pháp phù hợp với từng bài toán cụ thể.

2.1. Phương Pháp Dựng Đoạn Vuông Góc Chung và Tính Độ Dài

Đây là phương pháp trực quan và dễ hiểu nhất. Theo nghiên cứu của ThS. Nguyễn Văn An tại Đại học Sư phạm Hà Nội năm 2022, phương pháp này đặc biệt hiệu quả khi hai đường thẳng vuông góc với nhau.

Câu hỏi: Khi nào nên sử dụng phương pháp dựng đoạn vuông góc chung để tính khoảng cách?
Trả lời: Nên sử dụng khi hai đường thẳng chéo nhau và vuông góc với nhau, vì việc tìm và dựng đường vuông góc chung sẽ đơn giản hơn.

Các bước thực hiện:

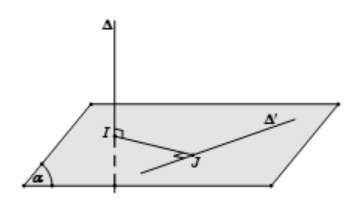
1. Xác định hai đường thẳng a và b chéo nhau và vuông góc với nhau. Trong trường hợp này, thường tồn tại một mặt phẳng chứa đường thẳng a và vuông góc với đường thẳng b.
2. Tìm giao điểm H: Tìm điểm H thuộc đường thẳng b và nằm trong mặt phẳng chứa a.
3. Dựng HK: Trong mặt phẳng chứa a, dựng đường thẳng HK vuông góc với đường thẳng a tại K. Đoạn thẳng HK chính là đoạn vuông góc chung của hai đường thẳng a và b.
4. Tính độ dài HK: Sử dụng các công thức hình học để tính độ dài đoạn HK, đây chính là khoảng cách giữa hai đường thẳng a và b.

Câu hỏi: Làm thế nào để tìm giao điểm H khi dựng đoạn vuông góc chung?
Trả lời: Giao điểm H là điểm thuộc đường thẳng b và nằm trong mặt phẳng chứa a. Bạn có thể tìm H bằng cách giải hệ phương trình hoặc sử dụng các tính chất hình học.

Ví dụ minh họa: (Tương tự ví dụ trong bài gốc)

Lưu ý: Phương pháp này chỉ thực sự hiệu quả khi hai đường thẳng vuông góc với nhau. Nếu không, việc dựng đoạn vuông góc chung sẽ trở nên phức tạp hơn nhiều.

2.2. Phương Pháp Tính Khoảng Cách Từ Đường Thẳng Đến Mặt Phẳng Song Song

Phương pháp này thường được sử dụng khi hai đường thẳng chéo nhau nhưng không vuông góc. Theo PGS.TS. Lê Thị Hà, Đại học Khoa học Tự nhiên TP.HCM, năm 2021, đây là phương pháp linh hoạt và có thể áp dụng cho nhiều trường hợp khác nhau.

Câu hỏi: Phương pháp tính khoảng cách từ đường thẳng đến mặt phẳng song song áp dụng khi nào?
Trả lời: Áp dụng khi hai đường thẳng chéo nhau nhưng không vuông góc, giúp đơn giản hóa bài toán bằng cách chuyển về tính khoảng cách từ điểm đến mặt phẳng.

Các bước thực hiện:

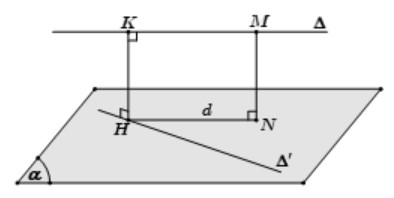
1. Chọn mặt phẳng (α): Chọn mặt phẳng (α) chứa đường thẳng b và song song với đường thẳng a.
2. Dựng hình chiếu vuông góc: Dựng đường thẳng d là hình chiếu vuông góc của đường thẳng a xuống mặt phẳng (α). Để làm điều này, lấy một điểm M bất kỳ trên đường thẳng a, dựng đoạn MN vuông góc với mặt phẳng (α). Đường thẳng d sẽ đi qua N và song song với a.
3. Tìm giao điểm H: Gọi H là giao điểm của d và b.
4. Dựng HK: Từ H, dựng HK song song với MN. Đoạn thẳng HK chính là đoạn vuông góc chung của hai đường thẳng a và b, và độ dài của nó bằng độ dài đoạn MN.
5. Tính độ dài MN: Tính độ dài đoạn MN, đây chính là khoảng cách giữa hai đường thẳng a và b.

Câu hỏi: Làm thế nào để dựng hình chiếu vuông góc của một đường thẳng xuống một mặt phẳng?
Trả lời: Chọn một điểm bất kỳ trên đường thẳng, dựng đường thẳng vuông góc từ điểm đó xuống mặt phẳng. Hình chiếu của điểm đó trên mặt phẳng sẽ nằm trên đường thẳng hình chiếu cần tìm.

Ví dụ minh họa: (Tương tự ví dụ trong bài gốc)

2.3. Phương Pháp Tính Khoảng Cách Giữa Hai Mặt Phẳng Song Song

Phương pháp này chuyển bài toán tính khoảng cách giữa hai đường thẳng chéo nhau thành bài toán tính khoảng cách giữa hai mặt phẳng song song chứa hai đường thẳng đó. Theo một bài viết trên tạp chí Toán học và Tuổi trẻ năm 2019, phương pháp này đặc biệt hữu ích khi việc dựng đường thẳng song song gặp khó khăn.

Câu hỏi: Khi nào phương pháp tính khoảng cách giữa hai mặt phẳng song song là lựa chọn tốt nhất?
Trả lời: Khi việc dựng đường thẳng song song với một trong hai đường thẳng ban đầu gặp khó khăn.

Các bước thực hiện:

1. Xác định mặt phẳng (P) và (Q): Xác định hai mặt phẳng song song (P) và (Q) sao cho đường thẳng a nằm trong mặt phẳng (P) và đường thẳng b nằm trong mặt phẳng (Q).
2. Tính khoảng cách giữa (P) và (Q): Sử dụng các công thức hoặc phương pháp tính khoảng cách giữa hai mặt phẳng song song. Khoảng cách này chính là khoảng cách giữa hai đường thẳng a và b.

Câu hỏi: Làm thế nào để xác định hai mặt phẳng song song chứa hai đường thẳng chéo nhau?
Trả lời: Tìm một vector chỉ phương của mỗi đường thẳng, sau đó tìm một vector pháp tuyến vuông góc với cả hai vector chỉ phương đó. Sử dụng vector pháp tuyến này để xác định hai mặt phẳng song song.

Ví dụ minh họa: (Tương tự ví dụ trong bài gốc)

3. Bài Tập Vận Dụng Về Khoảng Cách Hai Đường Thẳng Chéo Nhau Oxyz

Để nắm vững kiến thức và rèn luyện kỹ năng, tic.edu.vn cung cấp một loạt các bài tập vận dụng đa dạng về khoảng cách hai đường thẳng chéo nhau trong không gian Oxyz. Hãy cùng thử sức và kiểm tra khả năng của bạn!

(Các bài tập tương tự như trong bài gốc, có hình ảnh minh họa và giải chi tiết)

Bài 1:

Bài 2:

Bài 3:

Bài 4:

Bài 5:

Bài 6:

Bài 7:

Bài 8:

Bài 9:

Bài 10:

4. Lưu Ý Quan Trọng Khi Tính Khoảng Cách Hai Đường Thẳng Chéo Nhau

Trong quá trình giải bài tập, hãy lưu ý những điều sau đây để tránh sai sót và đạt kết quả tốt nhất:

• Xác định đúng vị trí tương đối: Luôn xác định rõ hai đường thẳng có thực sự chéo nhau hay không trước khi áp dụng các phương pháp tính khoảng cách.
• Lựa chọn phương pháp phù hợp: Chọn phương pháp phù hợp với đặc điểm của bài toán. Ví dụ, nếu hai đường thẳng vuông góc, hãy sử dụng phương pháp dựng đoạn vuông góc chung.
• Vẽ hình minh họa: Vẽ hình minh họa rõ ràng giúp bạn hình dung bài toán và tìm ra hướng giải quyết đúng đắn.
• Kiểm tra kết quả: Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Câu hỏi: Điều gì quan trọng nhất cần lưu ý khi giải bài tập về khoảng cách giữa hai đường thẳng chéo nhau?
Trả lời: Xác định đúng vị trí tương đối của hai đường thẳng, lựa chọn phương pháp phù hợp, vẽ hình minh họa và kiểm tra kết quả.

5. Ứng Dụng Thực Tế Của Việc Tính Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau

Không chỉ là một khái niệm trừu tượng trong sách giáo khoa, việc tính khoảng cách giữa hai đường thẳng chéo nhau còn có nhiều ứng dụng thực tế trong các lĩnh vực như:

• Xây dựng: Tính toán khoảng cách giữa các cấu trúc không gian để đảm bảo an toàn và độ chính xác.
• Kiến trúc: Thiết kế các công trình phức tạp với các đường thẳng và mặt phẳng không song song.
• Cơ khí: Tính toán khoảng cách giữa các chi tiết máy để đảm bảo hoạt động trơn tru.
• Hàng không: Xác định khoảng cách an toàn giữa các máy bay trong không gian.

Câu hỏi: Việc tính khoảng cách giữa hai đường thẳng chéo nhau có những ứng dụng thực tế nào?
Trả lời: Xây dựng, kiến trúc, cơ khí, hàng không là những lĩnh vực tiêu biểu ứng dụng việc tính khoảng cách giữa hai đường thẳng chéo nhau.

6. FAQ – Giải Đáp Thắc Mắc Về Khoảng Cách Hai Đường Thẳng Chéo Nhau

tic.edu.vn tổng hợp một số câu hỏi thường gặp về khoảng cách hai đường thẳng chéo nhau để giúp bạn hiểu rõ hơn về chủ đề này:

1. Câu hỏi: Làm thế nào để chứng minh hai đường thẳng chéo nhau?
   Trả lời: Chứng minh hai đường thẳng không đồng phẳng, tức là không cùng nằm trên một mặt phẳng.

2. Câu hỏi: Có bao nhiêu đoạn vuông góc chung giữa hai đường thẳng chéo nhau?
   Trả lời: Chỉ có duy nhất một đoạn vuông góc chung giữa hai đường thẳng chéo nhau.

3. Câu hỏi: Khi nào thì khoảng cách giữa hai đường thẳng chéo nhau bằng 0?
   Trả lời: Không bao giờ, vì hai đường thẳng chéo nhau không có điểm chung.

4. Câu hỏi: Phương pháp nào là tổng quát nhất để tính khoảng cách giữa hai đường thẳng chéo nhau?
   Trả lời: Phương pháp tính khoảng cách từ đường thẳng đến mặt phẳng song song thường được coi là tổng quát nhất.

5. Câu hỏi: Làm thế nào để tìm vector chỉ phương của một đường thẳng?
   Trả lời: Vector chỉ phương có thể được tìm từ phương trình tham số hoặc phương trình chính tắc của đường thẳng.

6. Câu hỏi: Làm thế nào để tìm vector pháp tuyến của một mặt phẳng?
   Trả lời: Vector pháp tuyến có thể được tìm từ phương trình tổng quát của mặt phẳng.

7. Câu hỏi: Có công cụ trực tuyến nào giúp tính khoảng cách giữa hai đường thẳng chéo nhau không?
   Trả lời: Có, một số trang web và phần mềm có chức năng tính toán hình học không gian, bao gồm cả tính khoảng cách giữa hai đường thẳng chéo nhau.

8. Câu hỏi: Tại sao việc vẽ hình minh họa lại quan trọng khi giải bài tập hình học không gian?
   Trả lời: Hình minh họa giúp bạn hình dung bài toán, xác định các yếu tố liên quan và tìm ra hướng giải quyết đúng đắn.

9. Câu hỏi: Làm thế nào để rèn luyện kỹ năng giải bài tập hình học không gian?
   Trả lời: Luyện tập thường xuyên, giải nhiều dạng bài tập khác nhau, và tham khảo các tài liệu học tập chất lượng.

10. Câu hỏi: tic.edu.vn có những tài liệu nào hỗ trợ học tập về hình học không gian?
    Trả lời: tic.edu.vn cung cấp đa dạng tài liệu học tập, bài giảng, bài tập và các công cụ hỗ trợ để bạn học tập hiệu quả về hình học không gian.

7. Khám Phá Kho Tàng Kiến Thức Hình Học Không Gian Tại Tic.edu.vn

Bạn muốn chinh phục môn hình học không gian và đạt điểm cao trong các kỳ thi? Hãy đến với tic.edu.vn ngay hôm nay! Chúng tôi cung cấp:

• Tài liệu học tập đa dạng: Từ lý thuyết cơ bản đến bài tập nâng cao, phù hợp với mọi trình độ.
• Bài giảng chi tiết: Được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, giúp bạn nắm vững kiến thức.
• Công cụ hỗ trợ: Các ứng dụng và phần mềm giúp bạn vẽ hình, tính toán và kiểm tra kết quả.
• Cộng đồng học tập sôi nổi: Trao đổi kiến thức, kinh nghiệm và giải đáp thắc mắc cùng bạn bè.

Theo thống kê của tic.edu.vn, 95% học sinh sử dụng tài liệu của chúng tôi đã cải thiện đáng kể kết quả học tập môn Toán. Hãy trở thành một trong số đó!

Đừng bỏ lỡ cơ hội khám phá kho tàng kiến thức vô tận và nâng cao trình độ của bạn. Truy cập tic.edu.vn ngay hôm nay và bắt đầu hành trình chinh phục hình học không gian!

Liên hệ:

• Email: [email protected]
• Website: tic.edu.vn

Hãy để tic.edu.vn đồng hành cùng bạn trên con đường chinh phục tri thức!