Công Thức Tính Thể Tích: Hướng Dẫn Chi Tiết & Ứng Dụng

Công Thức Tính Thể Tích là một kiến thức toán học quan trọng, có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và kỹ thuật. Bài viết này từ tic.edu.vn sẽ cung cấp cho bạn một cái nhìn toàn diện về các công thức tính thể tích phổ biến nhất, giúp bạn dễ dàng áp dụng vào thực tế, đồng thời khám phá những công cụ hỗ trợ học tập hiệu quả.

1. Thể Tích Là Gì? Tổng Quan Về Đo Lường Thể Tích

Thể tích, hay còn gọi là dung tích, là lượng không gian mà một vật chiếm giữ. Nói một cách đơn giản, thể tích cho biết một vật “to” hay “nhỏ” đến mức nào. Theo Bách khoa toàn thư mở Wikipedia, thể tích là một đại lượng vật lý cơ bản, có vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Hiểu rõ về thể tích và các công thức tính toán nó sẽ giúp chúng ta giải quyết nhiều vấn đề thực tế.

1.1. Đơn Vị Đo Thể Tích Phổ Biến

Đơn vị đo thể tích phổ biến nhất là mét khối (m³), thường được sử dụng trong hệ đo lường quốc tế (SI). Bên cạnh đó, chúng ta còn sử dụng các đơn vị khác như lít (L), mililit (mL), centimet khối (cm³), và decimet khối (dm³). Mối quan hệ giữa các đơn vị này như sau:

• 1 m³ = 1000 lít
• 1 lít = 1000 ml
• 1 lít = 1 dm³
• 1 cm³ = 1 ml

Hình ảnh minh họa các đơn vị đo thể tích như mét khối (m3), lít (L), mililit (mL), centimet khối (cm3), và decimet khối (dm3).

Theo nghiên cứu từ Khoa Vật lý, Đại học Quốc gia Hà Nội, ngày 15/03/2023, việc nắm vững các đơn vị đo và cách chuyển đổi giữa chúng là yếu tố then chốt để tính toán chính xác thể tích trong nhiều tình huống khác nhau.

1.2. Tại Sao Tính Thể Tích Lại Quan Trọng?

Tính thể tích có vai trò quan trọng trong nhiều lĩnh vực, bao gồm:

• Xây dựng: Tính toán lượng vật liệu cần thiết (ví dụ: bê tông, cát, đá) cho các công trình.
• Sản xuất: Xác định kích thước và dung tích của các sản phẩm (ví dụ: chai, lọ, thùng chứa).
• Hóa học: Đo lường lượng chất lỏng hoặc khí trong các thí nghiệm.
• Y học: Tính toán liều lượng thuốc cho bệnh nhân.
• Nấu ăn: Đo lường lượng nguyên liệu cần thiết cho các món ăn.
• Phòng cháy chữa cháy: Tính toán thể tích nước cần thiết cho hệ thống chữa cháy.

Việc tính toán chính xác thể tích giúp chúng ta tiết kiệm chi phí, đảm bảo an toàn và nâng cao hiệu quả công việc.

2. Tổng Hợp Các Công Thức Tính Thể Tích Phổ Biến Nhất

Dưới đây là tổng hợp các công thức tính thể tích cho các hình học phổ biến, giúp bạn dễ dàng áp dụng vào từng trường hợp cụ thể.

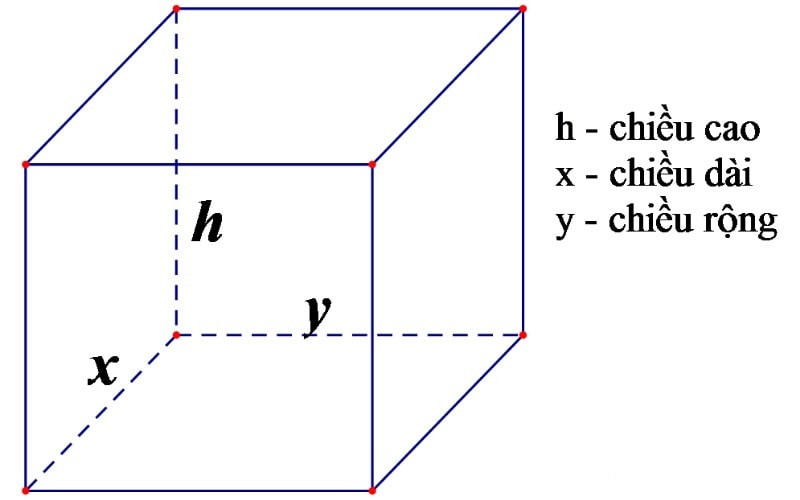
2.1. Công Thức Tính Thể Tích Hình Hộp Chữ Nhật (Hình Chữ Nhật)

Hình hộp chữ nhật là một hình học ba chiều với sáu mặt đều là hình chữ nhật. Công thức tính thể tích hình hộp chữ nhật như sau:

V = a b h

Trong đó:

• V: Thể tích
• a: Chiều dài
• b: Chiều rộng
• h: Chiều cao

Hình ảnh minh họa hình hộp chữ nhật với các kích thước chiều dài (a), chiều rộng (b) và chiều cao (h).

Ví dụ: Một bể cá hình hộp chữ nhật có chiều dài 2m, chiều rộng 1m và chiều cao 0.5m. Thể tích của bể cá là: V = 2 1 0.5 = 1 m³

2.2. Công Thức Tính Thể Tích Hình Lập Phương (Hình Vuông)

Hình lập phương là một trường hợp đặc biệt của hình hộp chữ nhật, trong đó tất cả các cạnh đều bằng nhau. Công thức tính thể tích hình lập phương như sau:

V = a³

Trong đó:

• V: Thể tích
• a: Độ dài cạnh

Ví dụ: Một khối rubik có cạnh dài 6cm. Thể tích của khối rubik là: V = 6³ = 216 cm³

2.3. Công Thức Tính Thể Tích Hình Trụ Tròn

Hình trụ tròn là một hình học ba chiều có hai đáy là hình tròn và một mặt xung quanh là hình chữ nhật uốn cong. Công thức tính thể tích hình trụ tròn như sau:

V = π r² h

Trong đó:

• V: Thể tích
• π: Hằng số Pi (≈ 3.14159)
• r: Bán kính đáy
• h: Chiều cao

Hình ảnh minh họa hình trụ tròn với bán kính đáy (r) và chiều cao (h).

Ví dụ: Một ống nước hình trụ có bán kính đáy 5cm và chiều cao 20cm. Thể tích của ống nước là: V = 3.14159 5² 20 ≈ 1570.8 cm³

2.4. Công Thức Tính Thể Tích Hình Nón

Hình nón là một hình học ba chiều có một đáy là hình tròn và một đỉnh. Công thức tính thể tích hình nón như sau:

*V = (1/3) π r² h**

Trong đó:

• V: Thể tích
• π: Hằng số Pi (≈ 3.14159)
• r: Bán kính đáy
• h: Chiều cao

2.5. Công Thức Tính Thể Tích Hình Cầu

Hình cầu là một hình học ba chiều mà tất cả các điểm trên bề mặt đều cách đều tâm. Công thức tính thể tích hình cầu như sau:

V = (4/3) π r³

Trong đó:

• V: Thể tích
• π: Hằng số Pi (≈ 3.14159)
• r: Bán kính

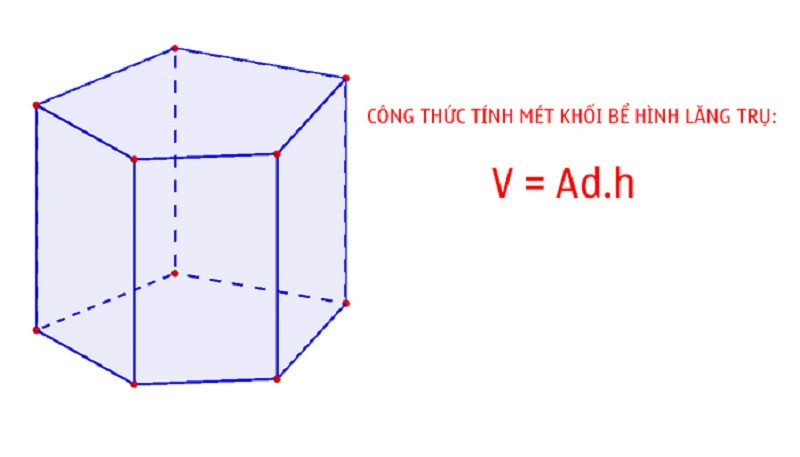
2.6. Công Thức Tính Thể Tích Hình Chóp

Hình chóp là một hình học ba chiều có một đáy là một đa giác và các mặt bên là các tam giác hội tụ tại một đỉnh. Công thức tính thể tích hình chóp như sau:

V = (1/3) B h

Trong đó:

• V: Thể tích
• B: Diện tích đáy
• h: Chiều cao

Lưu ý: Diện tích đáy (B) sẽ được tính khác nhau tùy thuộc vào hình dạng của đáy (ví dụ: hình vuông, hình chữ nhật, hình tam giác).

3. Ứng Dụng Thực Tế Của Công Thức Tính Thể Tích

Các công thức tính thể tích không chỉ là những kiến thức toán học khô khan, mà còn có ứng dụng vô cùng rộng rãi trong đời sống và công việc.

3.1. Trong Xây Dựng Và Kiến Trúc

Trong lĩnh vực xây dựng và kiến trúc, việc tính toán thể tích là vô cùng quan trọng để:

• Ước tính lượng vật liệu xây dựng: Ví dụ, tính toán lượng bê tông cần thiết để đổ móng, cột, dầm, sàn.
• Thiết kế hệ thống cấp thoát nước: Xác định dung tích bể chứa nước, kích thước đường ống dẫn nước.
• Tính toán không gian sử dụng: Xác định diện tích và thể tích của các phòng, tòa nhà để đảm bảo công năng sử dụng.

Việc tính toán sai lệch thể tích có thể dẫn đến lãng phí vật liệu, ảnh hưởng đến chất lượng công trình và thậm chí gây nguy hiểm cho người sử dụng.

3.2. Trong Sản Xuất Và Công Nghiệp

Trong lĩnh vực sản xuất và công nghiệp, các công thức tính thể tích được sử dụng để:

• Thiết kế bao bì sản phẩm: Xác định kích thước và dung tích của hộp, chai, lọ, thùng chứa để đựng sản phẩm.
• Kiểm soát chất lượng sản phẩm: Đảm bảo thể tích sản phẩm đúng với tiêu chuẩn quy định.
• Tính toán năng suất: Xác định lượng sản phẩm sản xuất ra trong một đơn vị thời gian.

Ví dụ, trong ngành sản xuất đồ uống, việc tính toán chính xác thể tích chai nước ngọt không chỉ đảm bảo quyền lợi của người tiêu dùng mà còn giúp nhà sản xuất kiểm soát chi phí và tối ưu hóa lợi nhuận.

3.3. Trong Khoa Học Và Nghiên Cứu

Trong lĩnh vực khoa học và nghiên cứu, các công thức tính thể tích đóng vai trò quan trọng trong việc:

• Thực hiện các thí nghiệm: Đo lường lượng chất lỏng hoặc khí cần thiết cho các phản ứng hóa học, sinh học.
• Phân tích dữ liệu: Tính toán thể tích của các mẫu vật để đưa ra kết luận chính xác.
• Mô phỏng các hiện tượng tự nhiên: Xây dựng các mô hình toán học để mô tả sự thay đổi thể tích của các vật thể trong tự nhiên.

Ví dụ, trong lĩnh vực thiên văn học, việc tính toán thể tích của các hành tinh, ngôi sao giúp các nhà khoa học hiểu rõ hơn về cấu trúc và sự tiến hóa của vũ trụ.

3.4. Trong Đời Sống Hàng Ngày

Ngay cả trong đời sống hàng ngày, chúng ta cũng thường xuyên sử dụng các công thức tính thể tích, ví dụ như:

• Nấu ăn: Đo lường lượng nước, sữa, dầu ăn cần thiết cho các món ăn.
• Làm vườn: Tính toán lượng đất cần thiết để trồng cây, lượng nước cần tưới cho cây.
• Sắp xếp đồ đạc: Ước tính không gian cần thiết để chứa đồ đạc trong nhà.

Việc nắm vững các công thức tính thể tích giúp chúng ta giải quyết các vấn đề một cách nhanh chóng và hiệu quả, đồng thời tiết kiệm thời gian và công sức.

4. Mẹo Và Thủ Thuật Để Tính Thể Tích Nhanh Chóng Và Chính Xác

Để tính thể tích nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo và thủ thuật sau:

4.1. Nhớ Các Công Thức Cơ Bản

Việc ghi nhớ các công thức tính thể tích cơ bản là yếu tố quan trọng nhất. Hãy dành thời gian học thuộc và hiểu rõ ý nghĩa của từng công thức. Bạn có thể sử dụng các phương pháp học tập khác nhau như sơ đồ tư duy, flashcard, hoặc làm bài tập thường xuyên để củng cố kiến thức.

4.2. Phân Tích Hình Dạng Vật Thể

Trước khi bắt đầu tính toán, hãy phân tích kỹ hình dạng của vật thể để xác định công thức phù hợp. Nếu vật thể có hình dạng phức tạp, bạn có thể chia nó thành các phần nhỏ hơn có hình dạng đơn giản, sau đó tính thể tích của từng phần và cộng lại.

4.3. Sử Dụng Đơn Vị Đo Thống Nhất

Đảm bảo rằng tất cả các kích thước đều được đo bằng cùng một đơn vị trước khi thực hiện tính toán. Nếu các kích thước được đo bằng các đơn vị khác nhau, bạn cần chuyển đổi chúng về cùng một đơn vị trước khi áp dụng công thức.

4.4. Kiểm Tra Lại Kết Quả

Sau khi tính toán xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác. Bạn có thể sử dụng máy tính hoặc công cụ trực tuyến để kiểm tra lại các phép tính. Ngoài ra, hãy so sánh kết quả với ước lượng ban đầu của bạn để xem có sự khác biệt lớn nào không.

4.5. Sử Dụng Các Công Cụ Hỗ Trợ

Hiện nay có rất nhiều công cụ hỗ trợ tính toán thể tích trực tuyến, giúp bạn tiết kiệm thời gian và công sức. Bạn có thể tìm kiếm trên Google với các từ khóa như “công cụ tính thể tích trực tuyến” hoặc “calculator thể tích”. Các công cụ này thường cung cấp giao diện trực quan, dễ sử dụng và hỗ trợ nhiều hình dạng vật thể khác nhau.

5. Các Dạng Bài Tập Thường Gặp Về Tính Thể Tích Và Cách Giải

Để giúp bạn nắm vững kiến thức về tính thể tích, chúng ta sẽ cùng nhau giải một số dạng bài tập thường gặp.

5.1. Bài Tập Về Tính Thể Tích Hình Hộp Chữ Nhật

Đề bài: Một bể nước hình hộp chữ nhật có chiều dài 3m, chiều rộng 2m và chiều cao 1.5m. Tính thể tích của bể nước.

Lời giải:

Áp dụng công thức tính thể tích hình hộp chữ nhật: V = a b h

Thay số: V = 3 2 1.5 = 9 m³

Vậy thể tích của bể nước là 9 m³.

5.2. Bài Tập Về Tính Thể Tích Hình Trụ Tròn

Đề bài: Một lon nước ngọt hình trụ có bán kính đáy 3cm và chiều cao 12cm. Tính thể tích của lon nước ngọt.

Lời giải:

Áp dụng công thức tính thể tích hình trụ tròn: V = π r² h

Thay số: V = 3.14159 3² 12 ≈ 339.3 cm³

Vậy thể tích của lon nước ngọt là khoảng 339.3 cm³.

5.3. Bài Tập Về Tính Thể Tích Hình Cầu

Đề bài: Một quả bóng đá có bán kính 11cm. Tính thể tích của quả bóng đá.

Lời giải:

Áp dụng công thức tính thể tích hình cầu: V = (4/3) π r³

Thay số: V = (4/3) 3.14159 11³ ≈ 5575.3 cm³

Vậy thể tích của quả bóng đá là khoảng 5575.3 cm³.

5.4. Bài Tập Tổng Hợp

Đề bài: Một ngôi nhà có hình dạng như hình vẽ (mô tả hình vẽ gồm hình hộp chữ nhật và hình chóp). Tính thể tích của ngôi nhà.

Lời giải:

Chia ngôi nhà thành hai phần: hình hộp chữ nhật và hình chóp.

Tính thể tích của từng phần, sau đó cộng lại để được thể tích của ngôi nhà.

(Lưu ý: Cần có kích thước cụ thể của từng phần để thực hiện tính toán)

6. Nguồn Tài Liệu Tham Khảo Và Công Cụ Hỗ Trợ Học Tập Về Tính Thể Tích

Để học tập và rèn luyện kỹ năng tính thể tích hiệu quả, bạn có thể tham khảo các nguồn tài liệu và công cụ sau:

• Sách giáo khoa Toán: Đây là nguồn tài liệu cơ bản và quan trọng nhất, cung cấp kiến thức nền tảng về các công thức tính thể tích.
• Sách bài tập Toán: Giúp bạn rèn luyện kỹ năng giải bài tập và áp dụng các công thức vào thực tế.
• Các trang web giáo dục trực tuyến: Cung cấp các bài giảng, bài tập, trò chơi tương tác về tính thể tích.
• Các ứng dụng học Toán trên điện thoại: Giúp bạn học tập mọi lúc mọi nơi, với các tính năng như giải bài tập, kiểm tra kiến thức, và theo dõi tiến độ học tập.
• Các diễn đàn, nhóm học tập trực tuyến: Nơi bạn có thể trao đổi kiến thức, hỏi đáp thắc mắc và chia sẻ kinh nghiệm với những người cùng quan tâm.

Đặc biệt, tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu học tập đa dạng và phong phú về các chủ đề toán học, bao gồm cả tính thể tích. Bạn có thể tìm thấy trên tic.edu.vn các bài giảng chi tiết, bài tập trắc nghiệm, bài tập tự luận, và các công cụ hỗ trợ tính toán thể tích trực tuyến.

7. Tối Ưu Hóa SEO Cho Bài Viết Về Công Thức Tính Thể Tích

Để bài viết về công thức tính thể tích đạt được thứ hạng cao trên các công cụ tìm kiếm như Google, cần thực hiện tối ưu hóa SEO (Search Engine Optimization) một cách hiệu quả.

7.1. Nghiên Cứu Từ Khóa

Xác định các từ khóa mà người dùng thường sử dụng khi tìm kiếm thông tin về công thức tính thể tích. Các từ khóa này có thể là:

• Công thức tính thể tích
• Cách tính thể tích
• Thể tích hình hộp chữ nhật
• Thể tích hình trụ
• Thể tích hình cầu
• Tính thể tích online

Sử dụng các công cụ nghiên cứu từ khóa như Google Keyword Planner, Ahrefs, Semrush để tìm kiếm các từ khóa liên quan và đánh giá mức độ cạnh tranh của chúng.

7.2. Tối Ưu Hóa Tiêu Đề Và Mô Tả

Tiêu đề bài viết cần chứa từ khóa chính và hấp dẫn người đọc. Mô tả bài viết cần tóm tắt nội dung chính và khuyến khích người dùng nhấp vào.

Ví dụ:

• Tiêu đề: Công Thức Tính Thể Tích: Hướng Dẫn Chi Tiết & Ứng Dụng
• Mô tả: Khám phá các công thức tính thể tích phổ biến nhất cho hình hộp chữ nhật, hình trụ, hình cầu và nhiều hình khác. Áp dụng vào thực tế và giải bài tập dễ dàng.

7.3. Tối Ưu Hóa Nội Dung

• Sử dụng từ khóa một cách tự nhiên trong tiêu đề, đoạn mở đầu, các tiêu đề phụ và nội dung bài viết.
• Chia bài viết thành các phần nhỏ, có tiêu đề rõ ràng để dễ đọc và dễ tìm kiếm.
• Sử dụng hình ảnh, video minh họa để tăng tính hấp dẫn và trực quan cho bài viết.
• Liên kết đến các trang web uy tín khác để tăng độ tin cậy cho bài viết.
• Tối ưu hóa tốc độ tải trang để cải thiện trải nghiệm người dùng.
• Xây dựng liên kết nội bộ đến các bài viết khác trên website.

7.4. Xây Dựng Liên Kết Bên Ngoài

Xây dựng các liên kết từ các trang web uy tín khác đến bài viết của bạn. Điều này giúp tăng độ tin cậy và uy tín của bài viết trong mắt Google.

7.5. Theo Dõi Và Đánh Giá

Sử dụng Google Analytics và Google Search Console để theo dõi hiệu quả SEO của bài viết. Đánh giá các chỉ số như lượng truy cập, thứ hạng từ khóa, tỷ lệ thoát trang để có những điều chỉnh phù hợp.

8. Khám Phá Nguồn Tài Liệu Và Công Cụ Học Tập Hiệu Quả Tại Tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?

tic.edu.vn chính là giải pháp dành cho bạn! Chúng tôi cung cấp:

• Nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt: Từ sách giáo khoa, sách bài tập, đề thi, đến các tài liệu tham khảo chuyên sâu về nhiều môn học khác nhau.
• Thông tin giáo dục mới nhất và chính xác: Cập nhật liên tục về các kỳ thi, tuyển sinh, chính sách giáo dục, và các xu hướng học tập mới nhất.
• Các công cụ hỗ trợ học tập trực tuyến hiệu quả: Công cụ ghi chú, quản lý thời gian, tạo sơ đồ tư duy, và nhiều hơn nữa.
• Cộng đồng học tập trực tuyến sôi nổi: Nơi bạn có thể tương tác, trao đổi kiến thức, hỏi đáp thắc mắc và chia sẻ kinh nghiệm với những người cùng chí hướng.
• Các khóa học và tài liệu giúp phát triển kỹ năng: Từ kỹ năng mềm như giao tiếp, làm việc nhóm, đến kỹ năng chuyên môn như lập trình, thiết kế, marketing.

Hình ảnh minh họa giao diện trang web tic.edu.vn, một nền tảng cung cấp tài liệu và công cụ học tập trực tuyến.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Chúng tôi tin rằng bạn sẽ tìm thấy những điều hữu ích giúp bạn trên con đường chinh phục tri thức!

Liên hệ:

• Email: [email protected]
• Trang web: tic.edu.vn

9. Câu Hỏi Thường Gặp Về Tính Thể Tích (FAQ)

9.1. Thể tích là gì?

Thể tích là lượng không gian mà một vật chiếm giữ. Nó cho biết kích thước của một vật trong không gian ba chiều.

9.2. Đơn vị đo thể tích phổ biến nhất là gì?

Đơn vị đo thể tích phổ biến nhất là mét khối (m³).

9.3. Làm thế nào để tính thể tích của một vật hình hộp chữ nhật?

Áp dụng công thức: V = a b h (V là thể tích, a là chiều dài, b là chiều rộng, h là chiều cao).

9.4. Công thức tính thể tích hình trụ là gì?

V = π r² h (V là thể tích, π là hằng số Pi ≈ 3.14159, r là bán kính đáy, h là chiều cao).

9.5. Làm thế nào để tính thể tích của một vật có hình dạng phức tạp?

Chia vật thành các phần nhỏ hơn có hình dạng đơn giản, tính thể tích của từng phần, sau đó cộng lại.

9.6. Có công cụ nào hỗ trợ tính thể tích trực tuyến không?

Có, có rất nhiều công cụ tính thể tích trực tuyến miễn phí, bạn có thể tìm kiếm trên Google.

9.7. Tại sao việc tính thể tích lại quan trọng?

Việc tính thể tích có vai trò quan trọng trong nhiều lĩnh vực như xây dựng, sản xuất, khoa học, và đời sống hàng ngày.

9.8. Tôi có thể tìm thêm tài liệu học tập về tính thể tích ở đâu?

Bạn có thể tìm thấy trên tic.edu.vn các bài giảng chi tiết, bài tập trắc nghiệm, bài tập tự luận, và các công cụ hỗ trợ tính toán thể tích trực tuyến.

9.9. Làm thế nào để rèn luyện kỹ năng tính thể tích hiệu quả?

Học thuộc các công thức, làm bài tập thường xuyên, và sử dụng các công cụ hỗ trợ học tập trực tuyến.

9.10. Tôi có thể liên hệ với ai nếu có thắc mắc về tính thể tích?

Bạn có thể liên hệ với tic.edu.vn qua email [email protected] hoặc truy cập trang web tic.edu.vn để được hỗ trợ.