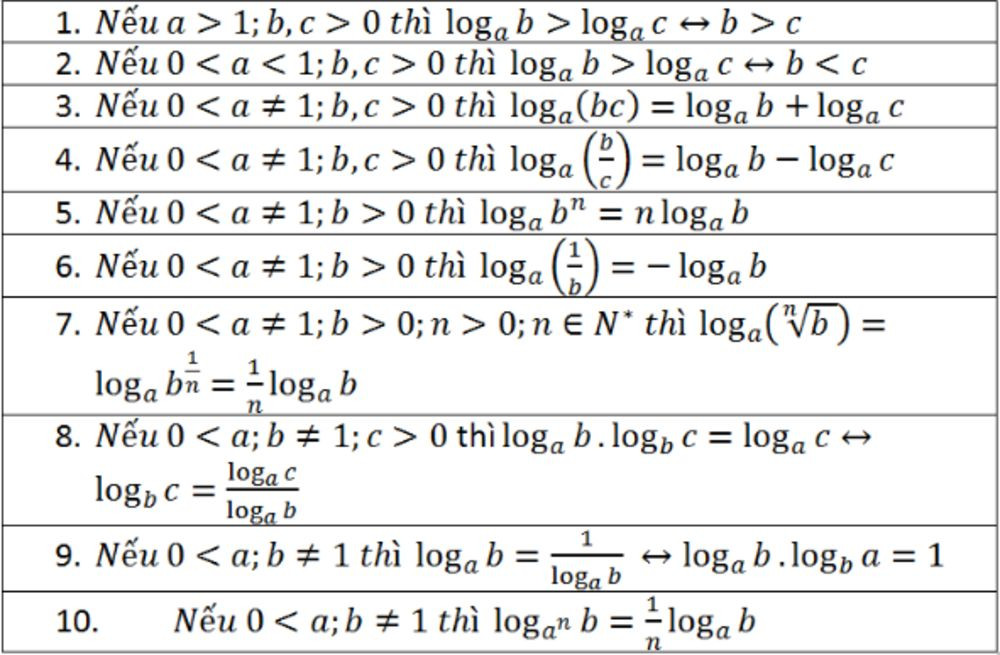
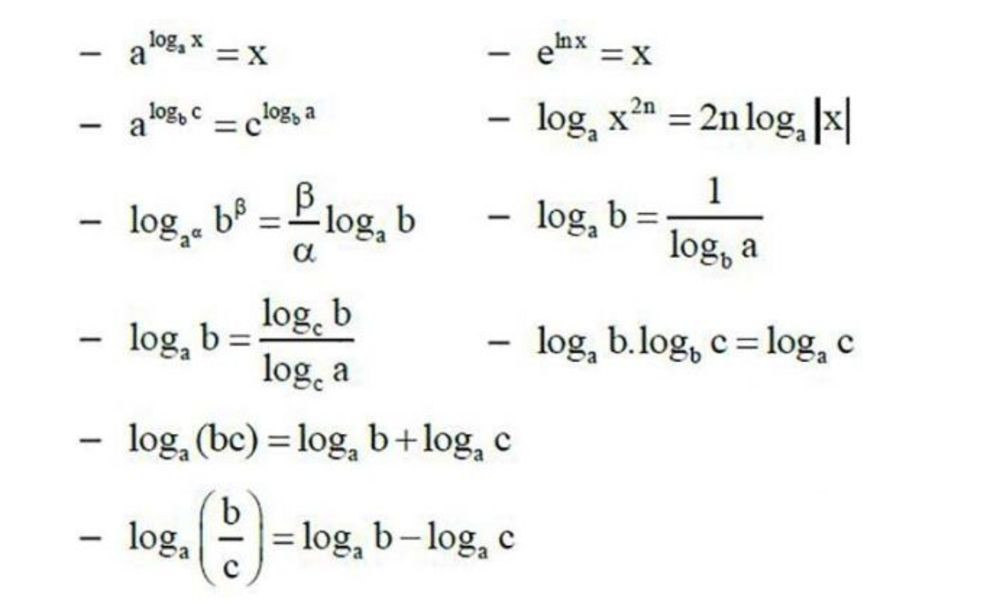
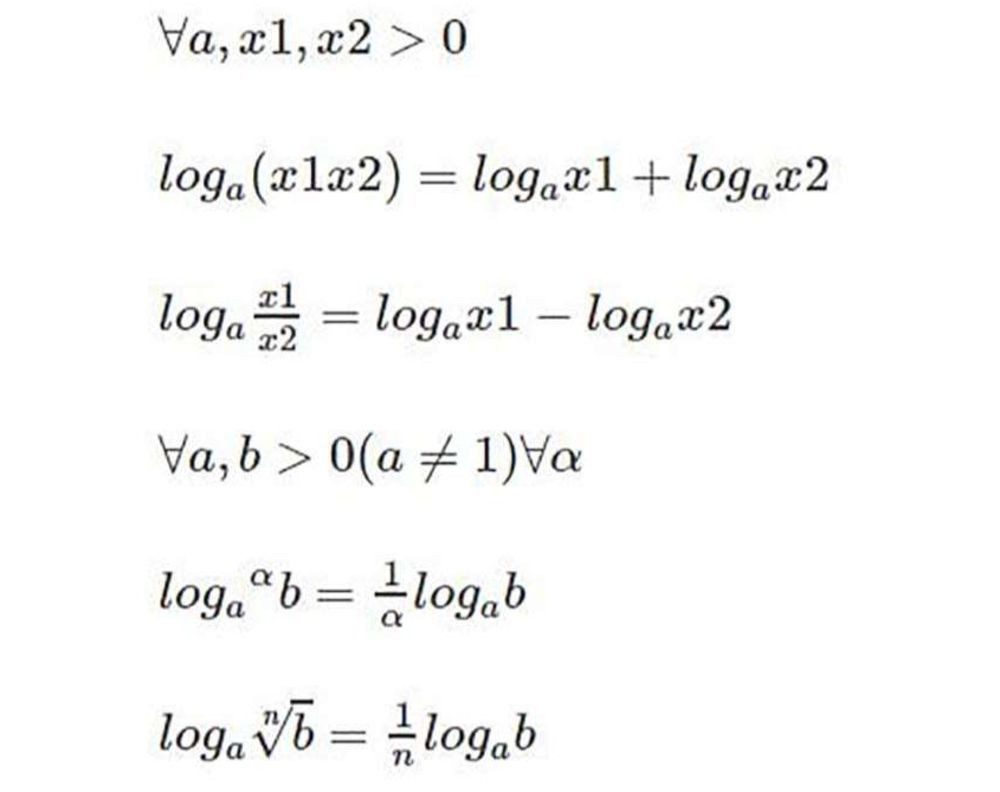
Cách Tính Logarit: Bí Quyết Chinh Phục Toán Học Hiệu Quả

Cách Tính Logarit là một kỹ năng toán học quan trọng, mở ra cánh cửa khám phá nhiều ứng dụng thực tế. Tại tic.edu.vn, chúng tôi cung cấp nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả để giúp bạn nắm vững kiến thức về logarit và ứng dụng chúng một cách thành thạo, từ đó chinh phục mọi bài toán liên quan đến hàm logarit và lũy thừa.

1. Khám Phá Bản Chất và Ứng Dụng Kỳ Diệu của Logarit

1.1. Logarit Là Gì? Định Nghĩa và Ý Nghĩa Sâu Sắc

Logarit, hay còn gọi là log, là phép toán nghịch đảo của lũy thừa. Hiểu một cách đơn giản, logarit của một số là số mũ mà cơ số (một giá trị cố định) cần được nâng lên để tạo ra số đó.

Ví dụ, logarit cơ số 2 của 8 là 3, vì 2³ = 8.

Logarit giúp chúng ta giải quyết các bài toán liên quan đến tìm số mũ, đặc biệt hữu ích trong các lĩnh vực khoa học, kỹ thuật, tài chính và nhiều lĩnh vực khác.

1.2. Lịch Sử Phát Triển Của Logarit: Từ Bảng Tính Đến Công Cụ Hiện Đại

Khái niệm logarit được John Napier giới thiệu vào đầu thế kỷ 17 như một công cụ hỗ trợ tính toán, đặc biệt là trong thiên văn học và hàng hải. Việc sử dụng bảng logarit giúp đơn giản hóa các phép nhân, chia phức tạp thành phép cộng và trừ, tiết kiệm đáng kể thời gian và công sức.

Theo nghiên cứu của Đại học St Andrews từ Khoa Lịch sử Toán học, vào năm 1614, John Napier đã xuất bản cuốn sách “Mirifici Logarithmorum Canonis Descriptio” (Mô tả về quy tắc tuyệt vời của logarit), đánh dấu bước khởi đầu cho sự phát triển của logarit.

Ngày nay, với sự phát triển của máy tính và các công cụ tính toán hiện đại, logarit vẫn giữ vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật, từ xử lý tín hiệu đến mật mã học.

1.3. Ứng Dụng Thực Tế Của Logarit: Vượt Ra Khỏi Sách Giáo Khoa

Logarit không chỉ là một khái niệm toán học trừu tượng, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và công việc:

• Trong tài chính: Tính lãi kép, phân tích tăng trưởng đầu tư.
• Trong khoa học: Đo độ pH của dung dịch, thang Richter đo độ lớn của động đất, độ ồn.
• Trong kỹ thuật: Xử lý tín hiệu, thiết kế mạch điện.
• Trong âm nhạc: Tính toán tần số âm thanh.
• Trong thống kê: Phân tích dữ liệu, xây dựng mô hình.

1.4. Các Loại Logarit Phổ Biến: Logarit Thập Phân, Logarit Tự Nhiên và Logarit Cơ Số Bất Kỳ

Có nhiều loại logarit khác nhau, tùy thuộc vào cơ số được sử dụng:

• Logarit thập phân (log₁₀): Cơ số là 10, thường được ký hiệu là log(x). Được sử dụng rộng rãi trong tính toán hàng ngày.
• Logarit tự nhiên (log_e): Cơ số là số Euler (e ≈ 2.71828), thường được ký hiệu là ln(x). Xuất hiện nhiều trong các bài toán giải tích và khoa học tự nhiên.
• Logarit cơ số bất kỳ (log_a): Cơ số là một số dương a khác 1.

Việc lựa chọn loại logarit phù hợp phụ thuộc vào bài toán cụ thể và mục đích sử dụng.

2. “Giải Mã” Các Tính Chất Quan Trọng Của Logarit

2.1. Tính Chất Cơ Bản Của Logarit: Nền Tảng Vững Chắc Để Giải Toán

Để giải quyết các bài toán logarit một cách hiệu quả, việc nắm vững các tính chất cơ bản là vô cùng quan trọng:

• log_a(1) = 0: Logarit của 1 với mọi cơ số đều bằng 0.
• log_a(a) = 1: Logarit của cơ số với chính nó bằng 1.
• *log_a(x y) = log_a(x) + log_a(y):** Logarit của một tích bằng tổng các logarit.
• log_a(x / y) = log_a(x) – log_a(y): Logarit của một thương bằng hiệu các logarit.
• *log_a(xⁿ) = n log_a(x):** Logarit của một lũy thừa bằng tích của số mũ và logarit.

2.2. Công Thức Đổi Cơ Số Logarit: “Chìa Khóa” Để Giải Quyết Bài Toán Khó

Công thức đổi cơ số logarit là một công cụ mạnh mẽ giúp chúng ta chuyển đổi giữa các loại logarit khác nhau:

log_b(x) = log_a(x) / log_a(b)

Trong đó:

• a là cơ số mới mà bạn muốn chuyển đổi sang.
• b là cơ số ban đầu.
• x là số cần tính logarit.

Công thức này đặc biệt hữu ích khi bạn cần tính logarit với một cơ số không có sẵn trên máy tính hoặc trong bảng logarit.

2.3. Các Hằng Đẳng Thức Logarit: “Vũ Khí” Bí Mật Để Rút Gọn Biểu Thức

Các hằng đẳng thức logarit là những công thức đặc biệt giúp chúng ta đơn giản hóa các biểu thức phức tạp chứa logarit:

• a^log_a(x) = x
• log_a(a^x) = x

Nắm vững và sử dụng linh hoạt các hằng đẳng thức này sẽ giúp bạn giải quyết các bài toán logarit một cách nhanh chóng và chính xác.

2.4. Lưu Ý Quan Trọng Khi Sử Dụng Tính Chất Logarit: Tránh Sai Lầm Đáng Tiếc

Khi áp dụng các tính chất và công thức logarit, cần lưu ý một số điều sau:

• Điều kiện xác định: Cơ số a phải dương và khác 1, đối số x phải dương.
• Thứ tự thực hiện phép tính: Ưu tiên các phép toán trong ngoặc, lũy thừa, nhân chia, cộng trừ.
• Kiểm tra kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

3. Hướng Dẫn Chi Tiết Cách Tính Logarit: Từ Cơ Bản Đến Nâng Cao

3.1. Tính Logarit Bằng Máy Tính: Nhanh Chóng và Tiện Lợi

Máy tính là công cụ hỗ trợ đắc lực trong việc tính toán logarit. Hầu hết các máy tính khoa học đều có chức năng tính logarit thập phân (log) và logarit tự nhiên (ln).

Để tính logarit cơ số bất kỳ, bạn có thể sử dụng công thức đổi cơ số:

log_b(x) = log(x) / log(b) hoặc log_b(x) = ln(x) / ln(b)

3.2. Tính Logarit Bằng Bảng Logarit: Phương Pháp Truyền Thống Vẫn Hiệu Quả

Mặc dù máy tính đã trở nên phổ biến, việc sử dụng bảng logarit vẫn là một kỹ năng hữu ích, giúp bạn hiểu rõ hơn về bản chất của logarit và rèn luyện khả năng tính toán.

Để sử dụng bảng logarit, bạn cần tìm giá trị logarit của số cần tính trong bảng, sau đó kết hợp với phần nguyên để có kết quả cuối cùng.

3.3. Tính Logarit Nhẩm: Rèn Luyện Tư Duy và Kỹ Năng Tính Toán

Trong một số trường hợp, bạn có thể tính nhẩm logarit bằng cách sử dụng các tính chất và công thức đã học. Ví dụ:

• Tính log₂(16): Vì 2⁴ = 16, nên log₂(16) = 4.
• Tính log(1000): Vì 10³ = 1000, nên log(1000) = 3.

3.4. Các Dạng Bài Tập Logarit Thường Gặp và Phương Pháp Giải Quyết

• Rút gọn biểu thức logarit: Sử dụng các tính chất và công thức để đơn giản hóa biểu thức.
• Giải phương trình logarit: Đưa phương trình về dạng cơ bản, sử dụng phép biến đổi tương đương hoặc đặt ẩn phụ.
• Giải bất phương trình logarit: Xác định điều kiện xác định, sử dụng tính chất đồng biến hoặc nghịch biến của hàm logarit.
• Ứng dụng logarit trong giải toán thực tế: Phân tích bài toán, xây dựng mô hình toán học và sử dụng logarit để giải quyết.

4. Mẹo Học và Ghi Nhớ Công Thức Logarit Hiệu Quả

4.1. Xây Dựng “Bản Đồ Tư Duy” Logarit: Hệ Thống Hóa Kiến Thức Một Cách Trực Quan

Sử dụng bản đồ tư duy (mind map) là một cách tuyệt vời để hệ thống hóa kiến thức về logarit một cách trực quan và dễ nhớ. Bạn có thể bắt đầu với khái niệm logarit ở trung tâm, sau đó phân nhánh ra các tính chất, công thức, ứng dụng và các dạng bài tập liên quan.

4.2. Học Bằng Hình Ảnh và Ví Dụ Minh Họa: Biến Khái Niệm Trừu Tượng Thành Dễ Hiểu

Thay vì chỉ học thuộc lòng các công thức, hãy cố gắng hiểu ý nghĩa của chúng thông qua các hình ảnh, ví dụ minh họa cụ thể. Điều này sẽ giúp bạn ghi nhớ kiến thức lâu hơn và biết cách áp dụng chúng vào thực tế.

4.3. Luyện Tập Thường Xuyên: “Mưa Dầm Thấm Lâu”, Nâng Cao Kỹ Năng Giải Toán

Không có cách học nào hiệu quả hơn việc luyện tập thường xuyên. Hãy làm nhiều bài tập logarit khác nhau, từ cơ bản đến nâng cao, để rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.

4.4. Tìm Hiểu Các Ứng Dụng Thực Tế: Tạo Động Lực Học Tập và Khám Phá

Khi bạn hiểu rõ về các ứng dụng thực tế của logarit, bạn sẽ cảm thấy hứng thú hơn với việc học và có động lực để khám phá sâu hơn về chủ đề này. Hãy tìm hiểu về cách logarit được sử dụng trong các lĩnh vực khoa học, kỹ thuật, tài chính và các lĩnh vực khác mà bạn quan tâm.

5. Các Sai Lầm Thường Gặp Khi Tính Logarit và Cách Khắc Phục

5.1. Nhầm Lẫn Giữa Các Tính Chất Logarit: Hậu Quả Khôn Lường

Một sai lầm phổ biến là nhầm lẫn giữa các tính chất logarit, dẫn đến kết quả sai lệch. Ví dụ, nhiều người nhầm lẫn giữa log_a(x + y) và log_a(x) + log_a(y).

Để tránh sai lầm này, hãy nắm vững các tính chất cơ bản và luyện tập thường xuyên để làm quen với chúng.

5.2. Quên Điều Kiện Xác Định: “Lỗi Chết Người” Trong Giải Toán

Việc quên điều kiện xác định của logarit (cơ số dương và khác 1, đối số dương) là một sai lầm nghiêm trọng, có thể dẫn đến kết quả vô nghĩa.

Hãy luôn kiểm tra điều kiện xác định trước khi bắt đầu giải bài toán logarit.

5.3. Tính Toán Sai Các Phép Toán Cơ Bản: Ảnh Hưởng Đến Kết Quả Cuối Cùng

Một sai sót nhỏ trong các phép toán cơ bản (cộng, trừ, nhân, chia) cũng có thể ảnh hưởng đến kết quả cuối cùng của bài toán logarit.

Hãy cẩn thận và kiểm tra kỹ lưỡng các phép tính để đảm bảo tính chính xác.

5.4. Sử Dụng Máy Tính Không Đúng Cách: Mất Đi Lợi Thế Của Công Cụ

Máy tính là một công cụ hữu ích, nhưng nếu sử dụng không đúng cách, nó có thể gây ra sai sót. Ví dụ, nhập sai công thức, quên đóng ngoặc hoặc sử dụng sai đơn vị.

Hãy đọc kỹ hướng dẫn sử dụng máy tính và luyện tập thường xuyên để sử dụng máy tính một cách hiệu quả.

6. Ứng Dụng Logarit Trong Giải Các Bài Toán Thực Tế

6.1. Bài Toán Về Lãi Kép: Tính Toán Tăng Trưởng Đầu Tư Hiệu Quả

Logarit được sử dụng để tính toán lãi kép, một khái niệm quan trọng trong tài chính. Công thức tính lãi kép như sau:

A = P (1 + r/n)^nt

Trong đó:

• A là số tiền cuối cùng.
• P là số tiền gốc.
• r là lãi suất hàng năm.
• n là số lần lãi được gộp trong một năm.
• t là số năm đầu tư.

Sử dụng logarit, chúng ta có thể giải quyết các bài toán liên quan đến tìm thời gian cần thiết để đạt được một mục tiêu tài chính nhất định.

6.2. Bài Toán Về Độ pH: Xác Định Tính Axit/Bazơ Của Dung Dịch

Độ pH của một dung dịch được định nghĩa là logarit âm của nồng độ ion hydro (H⁺):

pH = -log[H⁺]

Logarit giúp chúng ta biểu diễn nồng độ ion hydro một cách thuận tiện, vì nồng độ này thường rất nhỏ.

6.3. Bài Toán Về Thang Richter: Đo Độ Lớn Của Động Đất

Thang Richter là một thang logarit được sử dụng để đo độ lớn của động đất. Độ lớn M của một trận động đất được tính theo công thức:

M = log(A) – log(A₀)

Trong đó:

• A là biên độ tối đa ghi được trên máy đo địa chấn.
• A₀ là biên độ của một trận động đất chuẩn.

6.4. Bài Toán Về Độ Ồn: Đo Mức Độ Âm Thanh

Độ ồn được đo bằng đơn vị decibel (dB), sử dụng thang logarit. Mức độ âm thanh L được tính theo công thức:

*L = 10 log(I/I₀)**

Trong đó:

• I là cường độ âm thanh.
• I₀ là cường độ âm thanh chuẩn.

Logarit giúp chúng ta biểu diễn cường độ âm thanh một cách dễ quản lý, vì cường độ này có thể thay đổi rất lớn.

7. Logarit Trong Chương Trình Toán Phổ Thông

7.1. Logarit Ở Lớp 12: Kiến Thức Nền Tảng Cho Các Kỳ Thi Quan Trọng

Logarit là một chủ đề quan trọng trong chương trình toán lớp 12, xuất hiện trong cả chương trình cơ bản và nâng cao. Học sinh cần nắm vững các khái niệm, tính chất, công thức và ứng dụng của logarit để giải quyết các bài toán trong sách giáo khoa, bài kiểm tra và kỳ thi tốt nghiệp THPT.

Theo thống kê của Bộ Giáo dục và Đào tạo, các bài toán liên quan đến logarit chiếm khoảng 10-15% tổng số câu hỏi trong đề thi tốt nghiệp THPT môn Toán.

7.2. Các Dạng Bài Tập Logarit Thường Gặp Trong Đề Thi THPT Quốc Gia

Trong đề thi THPT Quốc gia, các bài tập logarit thường gặp bao gồm:

• Rút gọn biểu thức logarit: Yêu cầu sử dụng các tính chất và công thức để đơn giản hóa biểu thức.
• Giải phương trình, bất phương trình logarit: Yêu cầu tìm nghiệm của phương trình hoặc bất phương trình.
• Tìm tập xác định của hàm số logarit: Yêu cầu xác định khoảng giá trị của biến số để hàm số có nghĩa.
• Ứng dụng logarit trong giải toán thực tế: Yêu cầu vận dụng kiến thức logarit để giải quyết các bài toán liên quan đến lãi suất, độ pH, độ ồn, v.v.

7.3. Mẹo Ôn Thi Logarit Hiệu Quả: Bí Quyết Đạt Điểm Cao

• Nắm vững kiến thức cơ bản: Đảm bảo bạn hiểu rõ các khái niệm, tính chất và công thức logarit.
• Luyện tập thường xuyên: Làm nhiều bài tập khác nhau để rèn luyện kỹ năng giải toán.
• Hệ thống hóa kiến thức: Sử dụng bản đồ tư duy hoặc các phương pháp khác để tổ chức kiến thức một cách khoa học.
• Tìm hiểu các dạng bài tập thường gặp: Làm quen với các dạng bài tập trong đề thi THPT Quốc gia.
• Làm đề thi thử: Kiểm tra kiến thức và kỹ năng của bạn bằng cách làm các đề thi thử.

7.4. Tài Liệu Tham Khảo Logarit Chất Lượng Cao Tại Tic.edu.vn

Tại tic.edu.vn, chúng tôi cung cấp một kho tài liệu phong phú về logarit, bao gồm:

• Sách giáo khoa và sách bài tập: Đầy đủ kiến thức cơ bản và bài tập luyện tập.
• Tài liệu ôn thi THPT Quốc gia: Tổng hợp các dạng bài tập thường gặp và phương pháp giải.
• Bài giảng video: Giảng dạy chi tiết và dễ hiểu về logarit.
• Công cụ tính toán logarit trực tuyến: Hỗ trợ tính toán nhanh chóng và chính xác.

8. Logarit và Các Lĩnh Vực Khoa Học Khác

8.1. Logarit Trong Vật Lý: Mô Tả Các Hiện Tượng Tự Nhiên

Trong vật lý, logarit được sử dụng để mô tả nhiều hiện tượng tự nhiên, chẳng hạn như sự suy giảm phóng xạ, sự lan truyền sóng âm và ánh sáng.

Ví dụ, định luật Beer-Lambert mô tả sự hấp thụ ánh sáng của một dung dịch, sử dụng logarit để biểu diễn mối quan hệ giữa độ hấp thụ và nồng độ chất tan.

8.2. Logarit Trong Hóa Học: Tính Toán Nồng Độ và Tốc Độ Phản Ứng

Trong hóa học, logarit được sử dụng để tính toán nồng độ của các chất trong dung dịch, tốc độ phản ứng hóa học và hằng số cân bằng.

Độ pH, một đại lượng quan trọng trong hóa học, được định nghĩa là logarit âm của nồng độ ion hydro.

8.3. Logarit Trong Sinh Học: Mô Hình Hóa Tăng Trưởng Dân Số và Sự Tiến Hóa

Trong sinh học, logarit được sử dụng để mô hình hóa tăng trưởng dân số, sự tiến hóa của các loài và các quá trình sinh học khác.

Ví dụ, phương trình logistic mô tả sự tăng trưởng dân số giới hạn, sử dụng logarit để biểu diễn mối quan hệ giữa kích thước dân số và thời gian.

8.4. Logarit Trong Khoa Học Máy Tính: Phân Tích Thuật Toán và Xử Lý Dữ Liệu

Trong khoa học máy tính, logarit được sử dụng để phân tích độ phức tạp của các thuật toán, xử lý dữ liệu và xây dựng các mô hình học máy.

Ví dụ, thuật toán tìm kiếm nhị phân có độ phức tạp thời gian là O(log n), nghĩa là thời gian thực hiện thuật toán tăng theo logarit của kích thước dữ liệu.

9. Nguồn Tài Liệu và Công Cụ Hỗ Trợ Học Logarit Tại Tic.edu.vn

9.1. Kho Tài Liệu Phong Phú: Sách Giáo Khoa, Bài Tập, Đề Thi, Bài Giảng

Tic.edu.vn cung cấp một kho tài liệu phong phú về logarit, đáp ứng mọi nhu cầu học tập của bạn:

• Sách giáo khoa và sách bài tập: Đầy đủ kiến thức cơ bản và bài tập luyện tập.
• Đề thi thử THPT Quốc gia: Giúp bạn làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
• Bài giảng video: Giảng dạy chi tiết và dễ hiểu về logarit.
• Tài liệu tham khảo: Tổng hợp các kiến thức nâng cao và ứng dụng thực tế của logarit.

9.2. Công Cụ Tính Toán Logarit Trực Tuyến: Nhanh Chóng và Chính Xác

Chúng tôi cung cấp các công cụ tính toán logarit trực tuyến, giúp bạn giải quyết các bài toán logarit một cách nhanh chóng và chính xác:

• Máy tính logarit: Tính logarit với mọi cơ số.
• Công cụ giải phương trình logarit: Tìm nghiệm của phương trình logarit.
• Công cụ vẽ đồ thị hàm số logarit: Trực quan hóa hàm số logarit.

9.3. Cộng Đồng Học Tập Logarit: Trao Đổi, Chia Sẻ, Giải Đáp Thắc Mắc

Tham gia cộng đồng học tập logarit tại tic.edu.vn, bạn sẽ có cơ hội:

• Trao đổi kiến thức và kinh nghiệm với các bạn học khác.
• Đặt câu hỏi và nhận được sự giải đáp từ các chuyên gia.
• Chia sẻ tài liệu và nguồn học tập hữu ích.
• Tham gia các hoạt động học tập nhóm và các cuộc thi.

9.4. Đội Ngũ Hỗ Trợ Chuyên Nghiệp: Sẵn Sàng Giải Đáp Mọi Thắc Mắc

Nếu bạn có bất kỳ thắc mắc nào về logarit hoặc cần sự hỗ trợ trong quá trình học tập, đừng ngần ngại liên hệ với đội ngũ hỗ trợ chuyên nghiệp của chúng tôi. Chúng tôi luôn sẵn sàng giải đáp mọi thắc mắc của bạn một cách nhanh chóng và tận tình.

10. Câu Hỏi Thường Gặp Về Logarit (FAQ)

1. Logarit là gì và nó được sử dụng để làm gì?

Logarit là phép toán nghịch đảo của lũy thừa, dùng để tìm số mũ cần thiết để đạt được một giá trị nhất định. Nó được ứng dụng rộng rãi trong khoa học, kỹ thuật, tài chính và nhiều lĩnh vực khác.

2. Các loại logarit phổ biến là gì?

Các loại logarit phổ biến bao gồm logarit thập phân (cơ số 10), logarit tự nhiên (cơ số e) và logarit cơ số bất kỳ.

3. Làm thế nào để tính logarit bằng máy tính?

Hầu hết các máy tính khoa học đều có chức năng tính logarit thập phân (log) và logarit tự nhiên (ln). Để tính logarit cơ số bất kỳ, bạn có thể sử dụng công thức đổi cơ số.

4. Làm thế nào để sử dụng bảng logarit?

Để sử dụng bảng logarit, bạn cần tìm giá trị logarit của số cần tính trong bảng, sau đó kết hợp với phần nguyên để có kết quả cuối cùng.

5. Các tính chất cơ bản của logarit là gì?

Các tính chất cơ bản của logarit bao gồm: log_a(1) = 0, log_a(a) = 1, log_a(x y) = log_a(x) + log_a(y), log_a(x / y) = log_a(x) – log_a(y), log_a(xⁿ) = n log_a(x).

6. Công thức đổi cơ số logarit là gì và nó được sử dụng để làm gì?

Công thức đổi cơ số logarit là: log_b(x) = log_a(x) / log_a(b). Nó được sử dụng để chuyển đổi giữa các loại logarit khác nhau.

7. Làm thế nào để giải phương trình logarit?

Để giải phương trình logarit, bạn cần đưa phương trình về dạng cơ bản, sử dụng phép biến đổi tương đương hoặc đặt ẩn phụ.

8. Làm thế nào để tìm tập xác định của hàm số logarit?

Để tìm tập xác định của hàm số logarit, bạn cần xác định khoảng giá trị của biến số để hàm số có nghĩa (cơ số dương và khác 1, đối số dương).

9. Logarit được ứng dụng như thế nào trong tài chính?

Logarit được sử dụng để tính lãi kép, phân tích tăng trưởng đầu tư và giải quyết các bài toán liên quan đến tài chính.

10. Tôi có thể tìm thêm tài liệu và công cụ hỗ trợ học logarit ở đâu?

Bạn có thể tìm thấy rất nhiều tài liệu và công cụ hỗ trợ học logarit tại tic.edu.vn, bao gồm sách giáo khoa, bài tập, đề thi, bài giảng video, công cụ tính toán trực tuyến và cộng đồng học tập.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin, hay cần công cụ hỗ trợ học tập hiệu quả? Hãy đến với tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu phong phú, cập nhật, hữu ích và tham gia cộng đồng hỗ trợ học tập sôi nổi. Chúng tôi tin rằng với sự hỗ trợ của tic.edu.vn, bạn sẽ nắm vững kiến thức về logarit và đạt được thành công trong học tập.

Liên hệ với chúng tôi:

• Email: [email protected]
• Trang web: tic.edu.vn