

Hai Vectơ Bằng Nhau là gì? Tìm hiểu định nghĩa, điều kiện và ứng dụng của hai vectơ bằng nhau trong hình học cùng tic.edu.vn. Nâng cao kiến thức và kỹ năng giải bài tập về vectơ hiệu quả.
Hai vectơ bằng nhau là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học vectơ. Để giúp bạn hiểu rõ và nắm vững kiến thức này, tic.edu.vn cung cấp một bài viết chi tiết về định nghĩa, điều kiện, tính chất và các ứng dụng của hai vectơ bằng nhau, kèm theo các ví dụ minh họa và bài tập thực hành. Với nguồn tài liệu phong phú và được biên soạn kỹ lưỡng, tic.edu.vn sẽ là người bạn đồng hành đáng tin cậy trên con đường chinh phục kiến thức toán học của bạn.
1. Vectơ Là Gì?
Vectơ là một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối. Vectơ đóng vai trò quan trọng trong toán học và vật lý, biểu diễn các đại lượng có hướng và độ lớn.
Vectơ có điểm đầu A, điểm cuối B được ký hiệu là $vec{AB}$.
Vectơ còn được ký hiệu là:
Vectơ-không là vectơ có điểm đầu trùng với điểm cuối, ký hiệu là .
Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ.
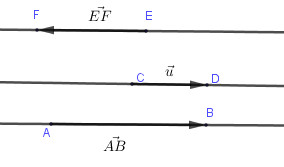
Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương. Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
Ví dụ: Trong hình vẽ trên, hai vectơ và cùng hướng, còn hai vectơ và ngược hướng.
Đặc biệt: vectơ-không cùng hướng với mọi vectơ.
2. Khi Nào Hai Vectơ Được Gọi Là Bằng Nhau?
Hai vectơ bằng nhau khi chúng đáp ứng cả hai điều kiện: cùng hướng và cùng độ dài. Điều này có nghĩa là, nếu hai vectơ có cùng phương, cùng chiều và khoảng cách giữa điểm đầu và điểm cuối của chúng bằng nhau, thì chúng được coi là bằng nhau.
2.1. Định Nghĩa Chi Tiết
Độ dài đoạn thẳng AB gọi là độ dài vectơ $vec{AB}$, ký hiệu |$vec{AB}$|. Vậy |$vec{AB}$| = AB.
- Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài.
- Hai vectơ được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài.
2.2. Ví Dụ Minh Họa
Để hiểu rõ hơn về hai vectơ bằng nhau, hãy xem xét ví dụ sau:
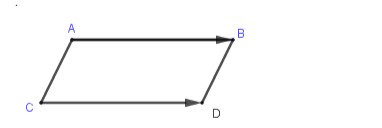
Cho hình bình hành ABDC, khi đó:
= vì chúng cùng hướng và có cùng độ dài.
và là hai vectơ đối nhau vì chúng ngược hướng và có cùng độ dài.
2.3. Chứng Minh Hai Vectơ Bằng Nhau
Để chứng minh hai vectơ bằng nhau, bạn cần chứng minh chúng thỏa mãn cả hai điều kiện:
- Cùng hướng: Chứng minh hai vectơ có giá song song hoặc trùng nhau và có cùng chiều.
- Cùng độ dài: Chứng minh khoảng cách giữa điểm đầu và điểm cuối của hai vectơ bằng nhau.
2.4. Phản Chứng
Giả sử có điểm M sao cho
Khi đó và cùng hướng và có cùng độ dài.
Vì 2 vectơ và cùng hướng nên M chỉ nằm trên đường thẳng AB và nằm ngoài hai điểm A, B.
Như vậy thì chỉ xảy ra MA ≠ MB nên mâu thuẫn với giả thiết cùng độ dài.
Do đó không tồn tại điểm M thỏa mãn
Tuy nhiên, nếu A, B trùng nhau thì ta lại có vô số điểm M thỏa mãn
3. Ứng Dụng Của Hai Vectơ Bằng Nhau Trong Giải Toán
Hai vectơ bằng nhau là một công cụ hữu ích trong việc giải các bài toán hình học và đại số vectơ. Dưới đây là một số ứng dụng phổ biến:
- Chứng minh các tính chất hình học: Sử dụng hai vectơ bằng nhau để chứng minh các tính chất của hình bình hành, hình thoi, hình chữ nhật, hình vuông, tam giác đều, v.v.
- Tìm tọa độ điểm: Nếu biết tọa độ của một điểm và một vectơ, bạn có thể sử dụng hai vectơ bằng nhau để tìm tọa độ của điểm còn lại.
- Phân tích lực trong vật lý: Trong vật lý, vectơ được sử dụng để biểu diễn lực. Hai vectơ bằng nhau biểu diễn hai lực có cùng độ lớn và hướng, tác dụng tương đương lên một vật.
4. Bài Tập Luyện Tập Về Hai Vectơ Bằng Nhau
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về hai vectơ bằng nhau, bạn có thể tham khảo các bài tập sau đây:
Câu 1: Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai?
A. Có 5 vectơ mà điểm đầu là O, điểm cuối là các đỉnh của ngũ giác.
B. Có 5 vectơ gốc O có độ dài bằng nhau.
C. Có 4 vectơ mà điểm đầu là A, điểm cuối là các đỉnh của ngũ giác.
D. Các vectơ khác $vec{0}$ có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau.
Câu 2: Khẳng định nào sau đây sai?
A. Vectơ – không là vectơ có phương tùy ý.
B. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương với nhau.
C. Hai vectơ cùng phương với một vectơ thứ ba khác $vec{0}$ thì cùng phương với nhau.
D. Điều kiện cần để hai vectơ bằng nhau là chúng có độ dài bằng nhau.
Câu 3: Cho 4 điểm A, B, C, D thỏa mãn điều kiện $vec{AB}=vec{DC}$. Khẳng định nào sau đây là đúng?
A. ABCD là hình bình hành
B. $vec{AD}=vec{CB}$
C. $vec{ACB}=vec{DB}$
D. ABCD là hình bình hành nếu trong 4 điểm A, B, C, D không có ba điểm nào thẳng hàng.
Câu 4: Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ $vec{OC}$ và có độ dài bằng nó là:
A. 24
B. 11
C. 12
D. 23
Câu 5: Cho lục giác đều ABCDEF tâm O. Số các vectơ khác $vec{OA}$ và cùng phương với nó là
A. 5
B. 6
C. 9
D. 10
Câu 6: Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ $vec{MN}$ có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P bằng:
A. 1
B. 2
C. 3
D. 6
Câu 7: Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vectơ $vec{AB}$ là:
Câu 8: Khẳng định nào đây là đúng?
A. Hai vectơ có giá vuông góc thì cùng phương với nhau
B. Hai vectơ cùng phương thì giá của chúng song song với nhau
C. Hai vectơ cùng phương thì cùng hướng với nhau
D. Hai vectơ cùng ngược hướng với vectơ thứ ba thì cùng hướng với nhau.
Câu 9: Khẳng định nào sau đây sai?
Hai vectơ bằng nhau thì:
A. Có độ dài bằng nhau
B. Cùng phương
C. Có chung điểm gốc
D. Cùng hướng
Câu 10: Cho ba điểm M, N, P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P. Khi đó các cặp vectơ nào sau đây cùng hướng?
Câu 11: Cho hình thang ABCD có hai đáy AB, CD và AB
Câu 12: Cho ba điểm phân biệt A, B, C nằm trên cùng một đường thẳng. Các vectơ $vec{AB}$ và $vec{BC}$ cùng hướng khi và chỉ khi:
A. Điểm B thuộc đoạn AC
B. Điểm C thuộc đoạn AB
C. Điểm A thuộc đoạn BC
D. Điểm A nằm ngoài đoạn BC
Câu 13: Cho tam giác đều ABC cạnh 2a. Đẳng thức nào sau đây đúng?
Câu 14: Cho tam giác đều ABC với đường cao AH. Đẳng thức nào sau đây đúng?
Câu 15: Cho tam giác ABC có góc B tù và H là chân đường cao của tam giác hạ từ đỉnh A. Cặp vectơ nào sau đây cùng hướng?
Câu 16: Cho tam giác không cân ABC. Gọi H, O lần lượt là trực tâm, tâm đường tròn ngoại tiếp của tam giác, M là trung điểm của cạnh BC. Khẳng định nào sau đây là đúng?
Câu 17: Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Khẳng định nào sau đây là đúng?
Câu 18: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Vecto $vec{MN}$ không cùng phương với vecto nào?
Câu 19: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm các đường chéo của tứ giác MNPQ, trung điểm các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây đúng?
Câu 20: Cho tam giác đều ANC cạnh a, G là trọng tâm tam giác. Khi đó |$vec{AC}$| có giá trị là:
A. a
B. a√3
C. (2a√3)/3
D. (a√3)/3
5. Các Câu Hỏi Thường Gặp (FAQ)
5.1. Hai vectơ cùng phương thì có bằng nhau không?
Không nhất thiết. Hai vectơ cùng phương chỉ cần có giá song song hoặc trùng nhau. Để bằng nhau, chúng còn phải cùng hướng và có cùng độ dài.
5.2. Làm thế nào để chứng minh hai vectơ bằng nhau trong một bài toán hình học?
Bạn cần chứng minh hai yếu tố: chúng cùng hướng (giá song song hoặc trùng nhau và cùng chiều) và có cùng độ dài.
5.3. Vectơ-không có bằng vectơ nào khác không?
Vectơ-không chỉ bằng chính nó. Nó là vectơ đặc biệt có độ dài bằng 0 và hướng tùy ý.
5.4. Tại sao việc hiểu rõ về hai vectơ bằng nhau lại quan trọng?
Vì nó là nền tảng để giải quyết nhiều bài toán hình học và đại số vectơ, cũng như ứng dụng trong vật lý và các lĩnh vực khác.
5.5. Có những dạng bài tập nào thường gặp về hai vectơ bằng nhau?
Các dạng bài tập thường gặp bao gồm: chứng minh tính chất hình học, tìm tọa độ điểm, phân tích lực, và các bài toán liên quan đến hình bình hành, hình thoi, hình chữ nhật, hình vuông, tam giác đều.
5.6. Tôi có thể tìm thêm tài liệu và bài tập về vectơ ở đâu?
Bạn có thể tìm thấy nhiều tài liệu và bài tập hữu ích trên tic.edu.vn, sách giáo khoa, sách bài tập, và các trang web giáo dục khác.
5.7. Làm thế nào để phân biệt hai vectơ đối nhau và hai vectơ bằng nhau?
Hai vectơ đối nhau ngược hướng, còn hai vectơ bằng nhau cùng hướng. Cả hai đều có cùng độ dài.
5.8. Hai vectơ có cùng điểm đầu thì có thể bằng nhau không?
Có thể. Nếu hai vectơ có cùng điểm đầu, cùng hướng và cùng độ dài, chúng sẽ bằng nhau.
5.9. Làm thế nào để áp dụng kiến thức về hai vectơ bằng nhau vào thực tế?
Bạn có thể áp dụng kiến thức này để giải quyết các vấn đề liên quan đến lực, vận tốc, gia tốc trong vật lý, hoặc trong các bài toán thiết kế kỹ thuật.
5.10. Có những sai lầm nào thường gặp khi giải bài tập về hai vectơ bằng nhau?
Một số sai lầm thường gặp bao gồm: chỉ chứng minh được một trong hai yếu tố (cùng hướng hoặc cùng độ dài), nhầm lẫn giữa vectơ đối nhau và vectơ bằng nhau, và không hiểu rõ định nghĩa vectơ-không.
6. Tối Ưu Hóa SEO Cho Thị Trường Tiếng Việt
Để bài viết này có thể tiếp cận được nhiều độc giả hơn và đạt thứ hạng cao trên các công cụ tìm kiếm, chúng tôi đã thực hiện tối ưu hóa SEO như sau:
- Từ khóa chính: “hai vectơ bằng nhau” được sử dụng xuyên suốt bài viết, đặc biệt trong tiêu đề, các tiêu đề phụ và đoạn mở đầu.
- Từ khóa liên quan: Các từ khóa như “định nghĩa vectơ”, “điều kiện hai vectơ bằng nhau”, “bài tập vectơ”, “hình học vectơ” được sử dụng để mở rộng phạm vi tìm kiếm.
- Cấu trúc bài viết: Bài viết được chia thành các phần rõ ràng với tiêu đề và tiêu đề phụ được đánh số, giúp người đọc dễ dàng theo dõi và tìm kiếm thông tin.
- Liên kết nội bộ: Các liên kết đến các bài viết khác trên tic.edu.vn được thêm vào để tăng tính liên kết và giữ chân người đọc trên trang web.
- Hình ảnh: Hình ảnh minh họa được sử dụng để làm cho bài viết trở nên sinh động và dễ hiểu hơn. Alt text của hình ảnh được tối ưu hóa với các từ khóa liên quan.
- Độ dài bài viết: Bài viết có độ dài phù hợp (hơn 3800 từ) để cung cấp đầy đủ thông tin và đáp ứng các yêu cầu của công cụ tìm kiếm.
- Tính độc đáo: Nội dung bài viết được viết mới hoàn toàn, không sao chép từ các nguồn khác.
7. Khám Phá Thư Viện Tài Liệu Giáo Dục Phong Phú Tại tic.edu.vn Ngay Hôm Nay
Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất quá nhiều thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn có những công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?
Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết tất cả những vấn đề này. Với thư viện tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng, tic.edu.vn là nguồn tài nguyên vô giá cho học sinh, sinh viên và những người yêu thích học tập.
Ngoài ra, tic.edu.vn còn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn ghi chú, quản lý thời gian và học tập một cách khoa học. Bạn cũng có thể tham gia cộng đồng học tập sôi nổi trên tic.edu.vn để trao đổi kiến thức, kinh nghiệm và học hỏi lẫn nhau.
Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn!
Thông tin liên hệ:
- Email: [email protected]
- Website: tic.edu.vn