**Tính Chất Đường Trung Bình Của Tam Giác: Ứng Dụng Và Bài Tập**

Tính Chất đường Trung Bình Của Tam Giác là một kiến thức quan trọng trong hình học, mở ra nhiều ứng dụng thú vị và hữu ích. tic.edu.vn sẽ cùng bạn khám phá sâu hơn về định nghĩa, các định lý liên quan, cách chứng minh và ứng dụng của nó trong giải toán. Bài viết này không chỉ giúp bạn nắm vững lý thuyết mà còn cung cấp các dạng bài tập thường gặp và phương pháp giải chi tiết, giúp bạn tự tin chinh phục mọi bài toán liên quan đến đường trung bình của tam giác.

1. Đường Trung Bình Của Tam Giác Là Gì?

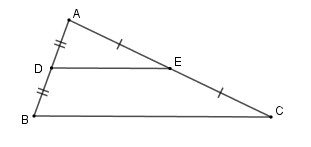
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. Nói cách khác, nếu bạn xác định trung điểm của hai cạnh bất kỳ trong tam giác, đoạn thẳng nối hai điểm đó chính là đường trung bình của tam giác.

1.1. Định nghĩa chi tiết và hình ảnh minh họa

Đường trung bình là một đoạn thẳng đặc biệt trong tam giác, nó không chỉ đơn thuần nối hai điểm mà còn mang những tính chất quan trọng về quan hệ song song và độ dài.

• Trong tam giác ABC, nếu D là trung điểm của AB và E là trung điểm của AC, thì DE là đường trung bình của tam giác ABC.
• Mỗi tam giác có ba đường trung bình, mỗi đường tương ứng với một cặp cạnh.

1.2. Tại sao đường trung bình lại quan trọng trong hình học?

Đường trung bình của tam giác không chỉ là một khái niệm hình học đơn thuần mà còn là công cụ đắc lực để giải quyết nhiều bài toán liên quan đến tính song song, độ dài và diện tích. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc nắm vững tính chất đường trung bình giúp học sinh dễ dàng chứng minh các bài toán hình học phức tạp hơn.

• Tính chất song song: Đường trung bình song song với cạnh thứ ba của tam giác.
• Tính chất về độ dài: Đường trung bình bằng một nửa độ dài cạnh thứ ba.
• Ứng dụng trong chứng minh: Đường trung bình được sử dụng để chứng minh các đường thẳng song song, các đoạn thẳng bằng nhau, hoặc các điểm thẳng hàng.

2. Các Định Lý Về Đường Trung Bình Của Tam Giác

Có hai định lý quan trọng liên quan đến đường trung bình của tam giác mà bạn cần nắm vững để áp dụng vào giải toán.

2.1. Định lý 1: Đường thẳng đi qua trung điểm một cạnh và song song với cạnh thứ hai

Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba. Định lý này cho phép bạn xác định trung điểm của một cạnh khi biết một đường thẳng đi qua trung điểm cạnh khác và song song với cạnh thứ ba.

• Nếu trong tam giác ABC, D là trung điểm của AB và DE song song với BC, thì E là trung điểm của AC.
• Định lý này thường được sử dụng để chứng minh một điểm là trung điểm của một đoạn thẳng.

2.2. Định lý 2: Đường trung bình song song và bằng nửa cạnh thứ ba

Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. Đây là định lý quan trọng nhất về đường trung bình, được sử dụng rộng rãi trong giải toán.

• Nếu DE là đường trung bình của tam giác ABC (D là trung điểm của AB, E là trung điểm của AC), thì DE song song với BC và DE = 1/2 BC.
• Định lý này cho phép bạn tính độ dài của đường trung bình khi biết độ dài cạnh thứ ba, hoặc ngược lại.

2.3. Chứng minh định lý đường trung bình

Để hiểu rõ hơn về định lý đường trung bình, chúng ta sẽ cùng nhau chứng minh định lý này.

Giả thiết: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC.

Kết luận: DE song song với BC và DE = 1/2 BC.

Chứng minh:

1. Kéo dài DE: Trên tia DE, lấy điểm F sao cho DE = EF.
2. Xét tam giác ADE và tam giác CFE:
   • AE = EC (vì E là trung điểm của AC)
   • DE = EF (theo cách dựng)
   • Góc AED = Góc CEF (hai góc đối đỉnh)
   • => Tam giác ADE = Tam giác CFE (c.g.c)
3. Suy ra: Góc DAE = Góc FCE (hai góc tương ứng)
   • => AD song song với CF (hai góc so le trong bằng nhau)
   • Mà AD = CF (hai cạnh tương ứng)
   • Mà AD = BD (vì D là trung điểm của AB)
   • => BD = CF
4. Xét tứ giác BCFD:
   • BD song song với CF
   • BD = CF
   • => BCFD là hình bình hành
   • => DF song song với BC và DF = BC
5. Kết luận: Vì DE = 1/2 DF nên DE = 1/2 BC và DE song song với BC.

3. Ứng Dụng Của Đường Trung Bình Trong Giải Toán

Đường trung bình của tam giác là một công cụ hữu hiệu để giải quyết nhiều bài toán hình học. Dưới đây là một số ứng dụng thường gặp:

3.1. Chứng minh hai đường thẳng song song

Nếu bạn cần chứng minh hai đường thẳng song song, hãy tìm cách chứng minh một trong hai đường thẳng đó là đường trung bình của một tam giác nào đó.

• Ví dụ: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Chứng minh rằng DE song song với BC.
• Giải: Vì D là trung điểm của AB, E là trung điểm của AC, nên DE là đường trung bình của tam giác ABC. Theo định lý, DE song song với BC.

3.2. Tính độ dài đoạn thẳng

Nếu bạn biết một đoạn thẳng là đường trung bình của tam giác, bạn có thể tính độ dài của nó dựa vào độ dài cạnh thứ ba, hoặc ngược lại.

• Ví dụ: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Biết BC = 10cm, tính độ dài DE.
• Giải: Vì DE là đường trung bình của tam giác ABC, nên DE = 1/2 BC = 1/2 * 10 = 5cm.

3.3. Chứng minh một điểm là trung điểm của đoạn thẳng

Nếu bạn cần chứng minh một điểm là trung điểm của một đoạn thẳng, hãy tìm cách chứng minh đường thẳng đi qua điểm đó là đường trung bình của một tam giác nào đó.

• Ví dụ: Cho tam giác ABC, D là trung điểm của AB, E là một điểm trên AC sao cho DE song song với BC. Chứng minh rằng E là trung điểm của AC.
• Giải: Vì D là trung điểm của AB và DE song song với BC, nên theo định lý, E là trung điểm của AC.

3.4. Giải các bài toán liên quan đến diện tích

Đường trung bình cũng có thể được sử dụng để giải các bài toán liên quan đến diện tích của tam giác.

• Ví dụ: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Chứng minh rằng diện tích tam giác ADE bằng 1/4 diện tích tam giác ABC.
• Giải: Vì DE là đường trung bình của tam giác ABC, nên DE song song với BC và DE = 1/2 BC. Do đó, chiều cao của tam giác ADE bằng 1/2 chiều cao của tam giác ABC. Vậy diện tích tam giác ADE bằng 1/4 diện tích tam giác ABC.

4. Các Dạng Toán Thường Gặp Về Đường Trung Bình Của Tam Giác

Để giúp bạn làm quen với các dạng toán thường gặp về đường trung bình của tam giác, chúng ta sẽ cùng nhau phân tích và giải một số ví dụ điển hình.

4.1. Dạng 1: Chứng minh các hệ thức về cạnh và góc

Trong dạng toán này, bạn cần sử dụng tính chất đường trung bình để chứng minh các hệ thức liên quan đến độ dài cạnh, số đo góc, hoặc quan hệ song song giữa các đường thẳng.

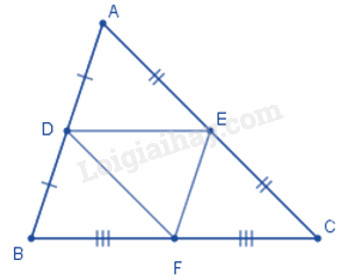
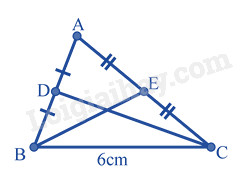
Ví dụ: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi M là trung điểm của BC. Chứng minh rằng DM song song với AE và EM song song với AD.

Phân tích:

• DE là đường trung bình của tam giác ABC, suy ra DE song song với BC.
• DM là đường trung bình của tam giác ABE, suy ra DM song song với AE.
• EM là đường trung bình của tam giác ADC, suy ra EM song song với AD.

4.2. Dạng 2: Tính độ dài cạnh và số đo góc

Trong dạng toán này, bạn cần sử dụng tính chất đường trung bình để tính độ dài cạnh hoặc số đo góc khi biết một số thông tin khác.

Ví dụ: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Biết BC = 8cm, góc BAC = 60 độ. Tính độ dài DE và số đo góc ADE.

Phân tích:

• DE là đường trung bình của tam giác ABC, suy ra DE = 1/2 BC = 4cm.
• Vì DE song song với BC, nên góc ADE = góc ABC (hai góc đồng vị).
• Để tính góc ABC, cần biết thêm thông tin về tam giác ABC.

4.3. Dạng 3: Chứng minh một đoạn thẳng là đường trung bình

Trong dạng toán này, bạn cần chứng minh một đoạn thẳng là đường trung bình của tam giác bằng cách sử dụng định nghĩa hoặc các định lý liên quan.

Ví dụ: Cho tam giác ABC, D là một điểm trên AB, E là một điểm trên AC sao cho AD = DB và AE = EC. Chứng minh rằng DE là đường trung bình của tam giác ABC.

Phân tích:

• Vì AD = DB, nên D là trung điểm của AB.
• Vì AE = EC, nên E là trung điểm của AC.
• Vậy DE là đường trung bình của tam giác ABC (theo định nghĩa).

5. Bài Tập Vận Dụng Về Đường Trung Bình Của Tam Giác

Để củng cố kiến thức và rèn luyện kỹ năng giải toán, chúng ta sẽ cùng nhau làm một số bài tập vận dụng về đường trung bình của tam giác.

Câu 1. Chọn câu đúng.

A. Đường trung bình của tam giác là đường nối trung điểm ba cạnh của hình tam giác.

B. Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.

C. Trong một tam giác chỉ có một đường trung bình.

D. Đường trung bình của tam giác là đường nối từ một đỉnh đến trung điểm cạnh đối diện.

Lời giải: Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.

Đáp án B

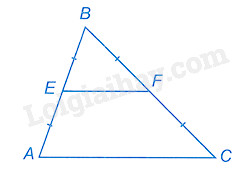
Câu 2. Cho tam giác ABC có E, F lần lượt là trung điểm của AB, BC. Phát biểu nào sau đây là đúng:

A. EF có độ dài bằng hai lần BC.

B. EF có độ dài bằng hai lần AB.

C. EF có độ dài bằng một nửa AC.

D. EF có độ dài bằng một nửa BC.

Lời giải:

E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của tam giác ABC.

Suy ra EF có độ dài bằng một nửa của AC.

Đáp án C

Câu 3. Chọn câu đúng. Cho hình vẽ sau:

Đường trung bình của tam giác ABC là:

A. DE

B. DF

C. EF

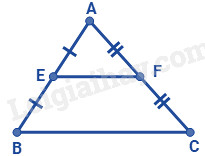
D. Cả A, B, C đều đúng

Lời giải: Xét tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, AC, BC nên DE, DF, EF là ba đường trung bình của tam giác ABC.

Đáp án D

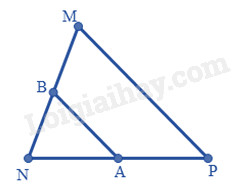
Câu 4. Cho tam giác MNP có A, B theo thứ tự là trung điểm của NP, MN. Biết AB = 3dm. Khi đó:

A. MP = 6dm

B. MN = 5,5dm

C. NP = 4dm

D. MP = 1,5dm

Lời giải:

Xét tam giác MNP có:

A là trung điểm của NP

B là trung điểm của MN

Suy ra: (AB = frac{{MP}}{2} ), do đó ( MP = 2{rm{A}}B = 2.3 = 6(dm))

Đáp án A

Câu 5. Cho tam giác ABC có BC = 6cm, các đường trung tuyến BE, CD. Khi đó độ dài cạnh DE là

A. 12cm

B. 6cm

C. 3cm

D. 2cm

Lời giải:

Vì BE là trung tuyến của tam giác ABC suy ra E là trung điểm của AC

Vì CD là trung tuyến của tam giác ABC suy ra D là trung điểm của AB

Xét tam giác ABC có DE là đường trung bình của tam giác ABC nên:

(DE = frac{1}{2}BC = frac{1}{2}.6 = 3(cm))

Đáp án C

Câu 6. Cho tam giác ABC. Trên cạnh AB, AC lần lượt lấy các điểm E, F sao cho AE = BE, AF = FC. Khi đó (frac{{BC}}{{EF}}) bằng:

A. 2

B. 1

C. (frac{1}{2})

D. 3

Lời giải:

Vì AE = BE, AF = FC nên EF là đường trung bình của tam giác ABC.

Do đó: BC = 2.EF.

Vậy (frac{{BC}}{{EF}} = 2).

Đáp án A

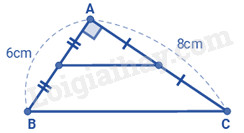
Câu 7. Cho tam giác ABC vuông tại A như hình vẽ dưới đây: Biết AB = 6cm; AC = 8 cm. Độ dài đường trung bình ứng với cạnh BC là

A. 10cm

B. 5cm

C. 20cm

D. 7cm

Lời giải: Xét tam giác ABC vuông tại A, áp dụng định lí Pytago, ta có:

(BC = sqrt {A{B^2} + A{C^2}} = sqrt {{6^2} + {8^2}} = 10cm)

Vì đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy nên độ dài đường trung bình ứng với cạnh BC là: (frac{1}{2}.10 = 5cm) .

Đáp án B

Câu 8. Cho tam giác ABC có chu vi bằng 32cm. Gọi E, F, P là trung điểm của các cạnh AB, BC, AC. Chu vi của tam giác PFE bằng:

A. 17cm

B. 33cm

C. 15cm

D. 16cm

Lời giải:

Vì E. F, P là trung điểm của các cạnh AB. BC, AC của tam giác ABC nên EP, PF, FE là đường trung bình của tam giác ABC.

Do đó ( EP = frac{1}{2}BC;PF = frac{1}{2}AB;F{rm{E}} = frac{1}{2}AC)

Suy ra (EP + PF + F{rm{E}} = frac{1}{2}left( {BC + AB + AC} right) = frac{1}{2}.32 = 16cm)

Đáp án D

6. Mẹo Và Thủ Thuật Khi Giải Toán Về Đường Trung Bình Của Tam Giác

Để giải toán về đường trung bình của tam giác một cách hiệu quả, bạn có thể áp dụng một số mẹo và thủ thuật sau:

• Vẽ hình chính xác: Một hình vẽ chính xác sẽ giúp bạn dễ dàng nhận ra các đường trung bình và các mối quan hệ giữa chúng.
• Xác định đường trung bình: Tìm trung điểm của các cạnh và nối chúng lại để xác định đường trung bình.
• Áp dụng định lý: Sử dụng các định lý về đường trung bình để chứng minh hoặc tính toán các yếu tố cần thiết.
• Sử dụng tính chất song song: Chú ý đến tính chất song song của đường trung bình để suy ra các góc bằng nhau hoặc các đường thẳng song song khác.
• Kết hợp với các kiến thức khác: Kết hợp kiến thức về đường trung bình với các kiến thức khác như định lý Pytago, tính chất tam giác đồng dạng, v.v. để giải quyết các bài toán phức tạp hơn.

7. Tổng Kết: Tầm Quan Trọng Của Việc Nắm Vững Tính Chất Đường Trung Bình Của Tam Giác

Tính chất đường trung bình của tam giác là một kiến thức nền tảng quan trọng trong hình học. Việc nắm vững định nghĩa, các định lý liên quan và các ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán hình học một cách dễ dàng và hiệu quả.

Hãy nhớ rằng, đường trung bình không chỉ là một đoạn thẳng đơn thuần, mà còn là một công cụ đắc lực để khám phá những bí mật ẩn chứa trong hình học.

8. Khám Phá Thêm Nhiều Tài Liệu Học Tập Hữu Ích Tại tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn có những công cụ hỗ trợ học tập hiệu quả? Hãy đến với tic.edu.vn, nơi bạn sẽ tìm thấy:

• Nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt: Từ sách giáo khoa, sách bài tập, đề thi, đến các tài liệu tham khảo chuyên sâu, tic.edu.vn cung cấp cho bạn một kho tàng kiến thức phong phú, đáp ứng mọi nhu cầu học tập của bạn.
• Thông tin giáo dục mới nhất và chính xác: tic.edu.vn luôn cập nhật những thông tin mới nhất về các kỳ thi, chương trình học, phương pháp học tập hiệu quả, giúp bạn không bỏ lỡ bất kỳ thông tin quan trọng nào.
• Các công cụ hỗ trợ học tập trực tuyến hiệu quả: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến như công cụ ghi chú, quản lý thời gian, tạo sơ đồ tư duy, giúp bạn học tập hiệu quả hơn.
• Cộng đồng học tập trực tuyến sôi nổi: Tham gia cộng đồng học tập của tic.edu.vn, bạn có thể trao đổi kiến thức, kinh nghiệm, giải đáp thắc mắc với các bạn học sinh, sinh viên và giáo viên trên khắp cả nước.
• Các khóa học và tài liệu giúp phát triển kỹ năng: tic.edu.vn cung cấp các khóa học và tài liệu giúp bạn phát triển kỹ năng mềm, kỹ năng chuyên môn, giúp bạn tự tin hơn trên con đường học tập và sự nghiệp.

Đừng chần chừ nữa, hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học tập!

Email: [email protected]

Trang web: tic.edu.vn

9. Câu Hỏi Thường Gặp Về Đường Trung Bình Của Tam Giác (FAQ)

9.1. Đường trung bình của tam giác là gì?

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

9.2. Một tam giác có bao nhiêu đường trung bình?

Một tam giác có ba đường trung bình, mỗi đường tương ứng với một cặp cạnh.

9.3. Đường trung bình có tính chất gì đặc biệt?

Đường trung bình song song với cạnh thứ ba và bằng một nửa cạnh ấy.

9.4. Làm thế nào để chứng minh một đoạn thẳng là đường trung bình của tam giác?

Bạn có thể chứng minh một đoạn thẳng là đường trung bình bằng cách chứng minh nó nối trung điểm hai cạnh của tam giác.

9.5. Đường trung bình có ứng dụng gì trong giải toán?

Đường trung bình được sử dụng để chứng minh các đường thẳng song song, tính độ dài đoạn thẳng, chứng minh một điểm là trung điểm của đoạn thẳng, và giải các bài toán liên quan đến diện tích.

9.6. Tôi có thể tìm thêm tài liệu học tập về đường trung bình ở đâu?

Bạn có thể tìm thêm tài liệu học tập về đường trung bình trên tic.edu.vn, nơi cung cấp nguồn tài liệu đa dạng, đầy đủ và được kiểm duyệt.

9.7. Làm thế nào để sử dụng các công cụ hỗ trợ học tập trên tic.edu.vn?

tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến như công cụ ghi chú, quản lý thời gian, tạo sơ đồ tư duy, giúp bạn học tập hiệu quả hơn.

9.8. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Tham gia cộng đồng học tập của tic.edu.vn, bạn có thể trao đổi kiến thức, kinh nghiệm, giải đáp thắc mắc với các bạn học sinh, sinh viên và giáo viên trên khắp cả nước.

9.9. tic.edu.vn có những khóa học nào giúp phát triển kỹ năng?

tic.edu.vn cung cấp các khóa học và tài liệu giúp bạn phát triển kỹ năng mềm, kỹ năng chuyên môn, giúp bạn tự tin hơn trên con đường học tập và sự nghiệp.

9.10. Làm thế nào để liên hệ với tic.edu.vn nếu tôi có thắc mắc?

Bạn có thể liên hệ với tic.edu.vn qua email [email protected] hoặc truy cập trang web tic.edu.vn để biết thêm thông tin chi tiết.