**Công Thức Các Hình: Tổng Hợp Chi Tiết Nhất, Ứng Dụng Thực Tế**

Bạn đang tìm kiếm một tài liệu đầy đủ và dễ hiểu về công thức tính diện tích các hình? Đừng lo lắng, tic.edu.vn sẽ giúp bạn! Bài viết này cung cấp một cái nhìn toàn diện, từ định nghĩa cơ bản đến các ứng dụng nâng cao, giúp bạn nắm vững kiến thức và tự tin chinh phục mọi bài toán hình học, đồng thời khám phá nhiều điều thú vị trong thế giới hình học.

1. Khám Phá Thế Giới Các Hình: Định Nghĩa và Tính Chất Cơ Bản

Trước khi đi sâu vào Công Thức Các Hình, hãy cùng tic.edu.vn điểm qua những kiến thức nền tảng về các hình học cơ bản, giúp bạn xây dựng một nền tảng vững chắc để học tập và ứng dụng hiệu quả.

1.1. Hình Tam Giác: “Viên Gạch” Của Hình Học

Hình tam giác là một đa giác có ba cạnh và ba đỉnh. Đây là một trong những hình học cơ bản nhất và có nhiều ứng dụng trong toán học và các lĩnh vực khác.

Minh họa hình tam giác với ba cạnh và ba đỉnh, nền tảng của hình học, theo tic.edu.vn

1.1.1. Phân Loại Tam Giác: Đa Dạng và Thú Vị

Tam giác có thể được phân loại dựa trên độ dài cạnh và số đo góc:

• Theo cạnh:
  • Tam giác đều: Ba cạnh bằng nhau, ba góc bằng 60 độ.
  • Tam giác cân: Ít nhất hai cạnh bằng nhau.
  • Tam giác thường: Ba cạnh khác nhau.
• Theo góc:
  • Tam giác nhọn: Ba góc nhọn (nhỏ hơn 90 độ).
  • Tam giác tù: Một góc tù (lớn hơn 90 độ).
  • Tam giác vuông: Một góc vuông (90 độ).

1.1.2. Tính Chất Tam Giác: “Chìa Khóa” Giải Bài Toán

Tam giác sở hữu nhiều tính chất quan trọng, giúp chúng ta giải quyết các bài toán hình học một cách hiệu quả:

• Tổng các góc: Tổng ba góc trong một tam giác luôn bằng 180 độ.
• Góc ngoài: Mỗi góc ngoài bằng tổng hai góc trong không kề với nó.
• Bất đẳng thức tam giác: Tổng độ dài hai cạnh bất kỳ luôn lớn hơn cạnh còn lại.
• Định lý Pythagoras: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
• Đường phân giác: Chia góc thành hai góc bằng nhau.
• Đường trung tuyến: Nối đỉnh với trung điểm cạnh đối diện.

1.2. Hình Vuông: Sự Hoàn Hảo Của Hình Học

Hình vuông là một tứ giác đều, có bốn cạnh bằng nhau và bốn góc vuông.

1.3. Hình Chữ Nhật: Nét Đẹp Của Sự Cân Đối

Hình chữ nhật là một tứ giác có bốn góc vuông và các cạnh đối diện bằng nhau.

1.4. Hình Bình Hành: Sự Linh Hoạt Trong Hình Học

Hình bình hành là một tứ giác có các cạnh đối diện song song và bằng nhau.

1.5. Hình Thang: Sự Kết Hợp Độc Đáo

Hình thang là một tứ giác có ít nhất một cặp cạnh đối diện song song.

1.6. Hình Tròn: Vẻ Đẹp Vĩnh Cửu

Hình tròn là tập hợp các điểm cách đều một điểm cố định (tâm).

2. “Bí Kíp” Tính Diện Tích Các Hình: Công Thức và Ứng Dụng

Tic.edu.vn sẽ “bật mí” những công thức tính diện tích các hình cơ bản nhất, kèm theo ví dụ minh họa dễ hiểu, giúp bạn áp dụng vào giải bài tập một cách thành thạo.

2.1. Diện Tích Tam Giác: Đa Dạng Cách Tính

2.1.1. Tam Giác Thường: “Linh Hoạt” Với Chiều Cao

Diện tích tam giác thường được tính bằng công thức:

S = (1/2) a h

Trong đó:

• a là độ dài cạnh đáy.
• h là chiều cao tương ứng với cạnh đáy.

Công thức diện tích tam giác thường, minh họa bởi tic.edu.vn

Ví dụ: Tam giác ABC có cạnh đáy BC = 6cm, chiều cao AH = 4cm. Diện tích tam giác ABC là: S = (1/2) 6 4 = 12 cm².

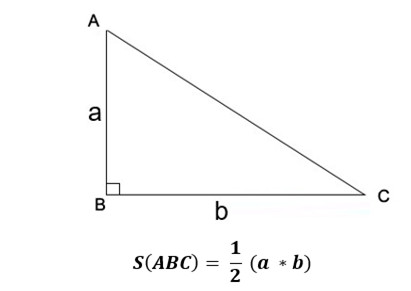
2.1.2. Tam Giác Vuông: “Đơn Giản” Với Cạnh Góc Vuông

Diện tích tam giác vuông được tính bằng công thức:

S = (1/2) a b

Trong đó:

• a và b là độ dài hai cạnh góc vuông.

Cách tính diện tích tam giác vuông theo tic.edu.vn

Ví dụ: Tam giác vuông ABC có cạnh AB = 3cm, cạnh AC = 4cm. Diện tích tam giác ABC là: S = (1/2) 3 4 = 6 cm².

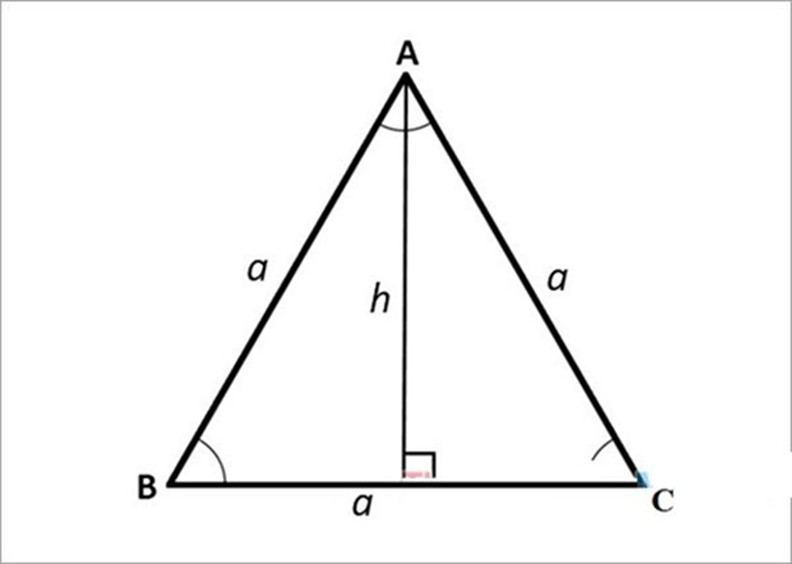
2.1.3. Tam Giác Cân: “Dễ Dàng” Với Cạnh Đáy và Chiều Cao

Diện tích tam giác cân được tính tương tự như tam giác thường:

S = (1/2) a h

Trong đó:

• a là độ dài cạnh đáy (cạnh khác hai cạnh bên).
• h là chiều cao tương ứng với cạnh đáy.

Công thức tính diện tích tam giác cân theo tic.edu.vn

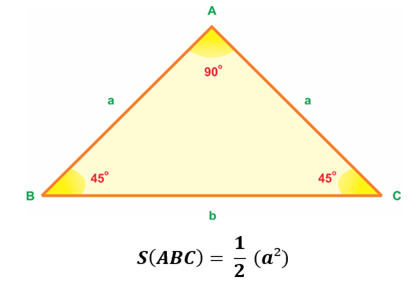
2.1.4. Tam Giác Đều: “Nhanh Chóng” Với Cạnh

Diện tích tam giác đều được tính bằng công thức:

S = (√3 / 4) * a²

Trong đó:

• a là độ dài cạnh.

Cách tính diện tích tam giác đều được minh họa bởi tic.edu.vn

2.1.5. Công Thức Heron: “Khi Biết 3 Cạnh”

Khi biết độ dài ba cạnh a, b, c của tam giác, ta có thể sử dụng công thức Heron để tính diện tích:

S = √[p(p – a)(p – b)(p – c)]

Trong đó:

• p là nửa chu vi của tam giác: p = (a + b + c) / 2

2.1.6. Diện tích tam giác trong Oxyz

Diện tích tam giác ABC được tính bằng nửa giá trị tuyệt đối của tích có hướng của hai vectơ AB và AC:

Công thức tính diện tích tam giác trong không gian Oxyz, một hướng dẫn từ tic.edu.vn

Trong đó: AB và AC là hai vectơ được biểu diễn trên trục Oxyz

Ví dụ: Trên hệ trục tọa độ cho tam giác ABC có 3 điểm A(-1; 1; 2), B(1; 2; 3), C(3; – 2; 0). Diện tích tam giác ABC được tính như sau:

2.2. Diện Tích Hình Vuông: “Dễ Nhớ” Với Cạnh

Diện tích hình vuông được tính bằng công thức:

S = a²

Trong đó:

• a là độ dài cạnh.

Ví dụ: Hình vuông ABCD có cạnh AB = 5cm. Diện tích hình vuông ABCD là: S = 5² = 25 cm².

2.3. Diện Tích Hình Chữ Nhật: “Quen Thuộc” Với Dài và Rộng

Diện tích hình chữ nhật được tính bằng công thức:

S = a * b

Trong đó:

• a là chiều dài.
• b là chiều rộng.

Ví dụ: Hình chữ nhật ABCD có chiều dài AB = 8cm, chiều rộng BC = 5cm. Diện tích hình chữ nhật ABCD là: S = 8 * 5 = 40 cm².

2.4. Diện Tích Hình Bình Hành: “Kết Hợp” Cạnh Đáy và Chiều Cao

Diện tích hình bình hành được tính bằng công thức:

S = a * h

Trong đó:

• a là độ dài cạnh đáy.
• h là chiều cao tương ứng với cạnh đáy.

2.5. Diện Tích Hình Thang: “Trung Bình Cộng” Hai Đáy

Diện tích hình thang được tính bằng công thức:

S = (1/2) (a + b) h

Trong đó:

• a và b là độ dài hai đáy.
• h là chiều cao (khoảng cách giữa hai đáy).

2.6. Diện Tích Hình Tròn: “Gắn Liền” Với Bán Kính

Diện tích hình tròn được tính bằng công thức:

S = π * r²

Trong đó:

• π (pi) là một hằng số, xấp xỉ bằng 3.14159.
• r là bán kính của hình tròn.

Ví dụ: Hình tròn có bán kính r = 4cm. Diện tích hình tròn là: S = π * 4² ≈ 50.27 cm².

3. Các Dạng Bài Tập Về Diện Tích Tam Giác: “Luyện Tập” Để Nâng Cao

Để giúp bạn nắm vững kiến thức và kỹ năng giải bài tập, tic.edu.vn tổng hợp các dạng bài tập thường gặp về diện tích tam giác, kèm theo hướng dẫn giải chi tiết.

3.1. Bài Tập Tính Diện Tích Khi Biết Cạnh Đáy và Chiều Cao

Đây là dạng bài tập cơ bản, bạn chỉ cần áp dụng trực tiếp công thức:

S = (1/2) a h

Ví dụ: Tam giác ABC có cạnh đáy BC = 10cm, chiều cao AH = 6cm. Tính diện tích tam giác ABC.

Lời giải: S = (1/2) 10 6 = 30 cm².

3.2. Bài Tập Tính Diện Tích Khi Biết Độ Dài Ba Cạnh

Với dạng bài tập này, bạn cần sử dụng công thức Heron:

S = √[p(p – a)(p – b)(p – c)]

Ví dụ: Tam giác ABC có độ dài ba cạnh AB = 5cm, BC = 7cm, CA = 8cm. Tính diện tích tam giác ABC.

Lời giải:

• Tính nửa chu vi: p = (5 + 7 + 8) / 2 = 10 cm
• Áp dụng công thức Heron: S = √[10(10 – 5)(10 – 7)(10 – 8)] = √(10 5 3 * 2) = √300 ≈ 17.32 cm².

3.3. Bài Tập Tính Diện Tích Tam Giác Đều Khi Biết Một Cạnh

Bạn có thể áp dụng công thức:

S = (√3 / 4) * a²

Ví dụ: Tam giác đều ABC có cạnh AB = 4cm. Tính diện tích tam giác ABC.

Lời giải: S = (√3 / 4) * 4² = 4√3 ≈ 6.93 cm².

Ngoài ra, bạn có thể giải bài tập này bằng cách tìm chiều cao của tam giác đều, sau đó áp dụng công thức tính diện tích tam giác thường.

3.4. Bài Tập Tính Diện Tích Tam Giác Vuông Khi Biết Hai Cạnh Góc Vuông

Áp dụng công thức:

S = (1/2) a b

Ví dụ: Tam giác vuông ABC có cạnh AB = 6cm, cạnh AC = 8cm. Tính diện tích tam giác ABC.

Lời giải: S = (1/2) 6 8 = 24 cm².

3.5. Bài Tập Tính Diện Tích Tam Giác Trong Tọa Độ Oxyz

Bạn cần tìm tọa độ của hai vectơ AB và AC, sau đó tính tích có hướng của hai vectơ này. Diện tích tam giác bằng một nửa độ dài của tích có hướng.

3.6. Bài Tập Tìm Độ Dài Cạnh Khi Biết Diện Tích

Trong dạng bài tập này, bạn cần sử dụng công thức diện tích để thiết lập phương trình, sau đó giải phương trình để tìm độ dài cạnh cần tìm.

3.7. Bài Tập Tính Diện Tích Tam Giác Khi Biết Chu Vi và Bán Kính Đường Tròn Nội Tiếp

Để tính diện tích tam giác khi biết chu vi (P) và bán kính đường tròn nội tiếp (r), ta sử dụng một công thức liên quan đến tam giác và đường tròn nội tiếp.

Đặt a, b và c lần lượt là ba cạnh của tam giác và R là bán kính đường tròn ngoại tiếp tam giác (được tính bằng ba đỉnh của tam giác). Ta có các mối quan hệ sau:

1. Diện tích tam giác (S) và bán kính đường tròn ngoại tiếp (R):

S = (abc) / (4R)

2. Diện tích tam giác (S) và chu vi (P):

S = (P * r) / 2

4. Bài Tập Mẫu Về Diện Tích Tam Giác: “Tham Khảo” Để Hiểu Sâu

4.1. Bài Tập 1

Tam giác ABC vuông tại A, có chiều cao AH = 4cm, cạnh BC = 8cm. Tính diện tích tam giác ABC.

Lời giải:

Vì tam giác ABC vuông tại A, ta có AH là đường cao ứng với cạnh huyền BC.

Diện tích tam giác ABC là: S = (1/2) AH BC = (1/2) 4 8 = 16 cm².

4.2. Bài Tập 2

Tam giác ABC có độ dài ba cạnh AB = 6cm, BC = 8cm, CA = 10cm. Chứng minh tam giác ABC vuông tại A và tính diện tích tam giác ABC.

Lời giải:

• Ta có: AB² + AC² = 6² + 8² = 36 + 64 = 100 = BC²
• Vậy tam giác ABC vuông tại A (theo định lý Pythagoras đảo).
• Diện tích tam giác ABC là: S = (1/2) AB AC = (1/2) 6 8 = 24 cm².

4.3. Bài Tập 3

Tam giác ABC có chu vi P = 24cm, bán kính đường tròn nội tiếp r = 2cm. Tính diện tích tam giác ABC.

Lời giải:

Diện tích tam giác ABC là: S = (P r) / 2 = (24 2) / 2 = 24 cm².

5. Câu Hỏi Thường Gặp (FAQ): “Giải Đáp” Mọi Thắc Mắc

Tic.edu.vn hiểu rằng bạn có thể có nhiều câu hỏi trong quá trình học tập. Dưới đây là một số câu hỏi thường gặp về diện tích tam giác, kèm theo câu trả lời chi tiết.

5.1. Cách Tính Diện Tích Tam Giác Lớp 5?

Công thức tính diện tích tam giác lớp 5 là:

S = (1/2) a h

Trong đó:

• a là độ dài cạnh đáy.
• h là chiều cao tương ứng với cạnh đáy.

Công thức này áp dụng được cho tam giác thường, tam giác cân, tam giác vuông.

5.2. Tính Diện Tích Tam Giác Khi Biết 3 Cạnh?

Khi biết độ dài ba cạnh của tam giác, bạn có thể sử dụng công thức Heron để tính diện tích:

S = √[p(p – a)(p – b)(p – c)]

Trong đó:

• p là nửa chu vi của tam giác: p = (a + b + c) / 2

5.3. Làm Thế Nào Để Nhớ Các Công Thức Tính Diện Tích Tam Giác?

Để nhớ các công thức tính diện tích tam giác, bạn nên:

• Hiểu rõ ý nghĩa của từng công thức.
• Luyện tập giải nhiều bài tập khác nhau.
• Tự tạo ra các ví dụ minh họa.
• Sử dụng các phương pháp học tập trực quan (ví dụ: sơ đồ tư duy).

6. Ưu Điểm Vượt Trội Của Tic.edu.vn: “Người Bạn Đồng Hành” Đáng Tin Cậy

Tic.edu.vn tự hào là một nguồn tài liệu học tập chất lượng và đáng tin cậy, mang đến cho bạn những lợi ích vượt trội:

• Đa dạng: Cung cấp đầy đủ công thức các hình và kiến thức liên quan.
• Cập nhật: Thông tin mới nhất về giáo dục và phương pháp học tập.
• Hữu ích: Hướng dẫn chi tiết, dễ hiểu, giúp bạn áp dụng vào thực tế.
• Cộng đồng: Tạo môi trường học tập trực tuyến sôi nổi, nơi bạn có thể trao đổi kiến thức và kinh nghiệm với những người cùng chí hướng.

7. Lời Kêu Gọi Hành Động (CTA): Khám Phá Tic.edu.vn Ngay Hôm Nay!

Bạn còn chần chừ gì nữa? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học vấn!

Thông tin liên hệ:

• Email: [email protected]
• Trang web: tic.edu.vn

Hãy để tic.edu.vn trở thành “người bạn đồng hành” đáng tin cậy trên hành trình khám phá tri thức của bạn!

Ý định tìm kiếm của người dùng:

1. Tìm kiếm công thức tính diện tích các hình cơ bản: Người dùng muốn tìm một danh sách đầy đủ các công thức tính diện tích hình vuông, hình chữ nhật, hình tròn, tam giác, hình bình hành, hình thang.
2. Tìm kiếm công thức tính diện tích tam giác: Người dùng muốn tìm các công thức tính diện tích tam giác khác nhau, bao gồm tam giác thường, tam giác vuông, tam giác cân, tam giác đều.
3. Tìm kiếm cách tính diện tích hình học không gian: Người dùng muốn tìm hiểu về cách tính diện tích các hình khối trong không gian ba chiều.
4. Tìm kiếm ví dụ minh họa về cách tính diện tích: Người dùng muốn xem các ví dụ cụ thể về cách áp dụng công thức tính diện tích vào giải các bài toán thực tế.
5. Tìm kiếm tài liệu học tập về diện tích các hình: Người dùng muốn tìm kiếm các tài liệu học tập, bài giảng, bài tập về diện tích các hình để ôn tập và nâng cao kiến thức.